Cho tam giác ABC lấy m là trung điểm BC. Trên tia AM lấy điểm A sao cho m là trung điểm của của AH
DT
Những câu hỏi liên quan
Cho tam giác ABC nhọn (AB< AC). Gọi M là trung điểm của BC. Trên tia AM lấy điểm N sao cho M là trung điểm của AN. a. Chứng minh tam giác AMB = tam giác NMC b. Vẽ AH vuông góc BC(H thuộc BC), trên tia đối của tia HA lấy điểm I sao cho HI = HA. Chứng minh: tam giác ABI cân và BI = CN
a: Xét ΔAMB và ΔNMC có
MA=MN
góc AMB=góc NMC
MB=MC
Do đó: ΔAMB=ΔNMC
b: Xét ΔBAI có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAI cân tại B
=>BA=BI=CN
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC). Kẻ AH vuông góc BC tại H, trên tia AH lấy điểm M sao cho H là trung điểm AM. a) Chứng minh: AABH = AMBH b) Chứng minh: BẠC BMC c) Gọi I là trung điểm BC, trên tia đối của tia IA lấy điểm D sao cho I là trung điểm AD.Chứng minh:DC//AB
Bài 4: (3,5 điểm)
Cho tam giác ABC có ba góc nhọn ( AB < AC), M là trung điểm của cạnh BC. Trên tia AM lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh: ∆AMB = ∆DMC
b) Chứng minh : AB//CD
c) Kẻ AH vuông góc với BC tại H trên tia AH lấy điểm K sao cho H là trung điểm của AK. Chứng minh MH là phân giác của góc AMK
a/ Xét △ABM và △DMC có:
AM=MD(gt)
MB=MC(gt)
^AMB=^CMD(đối đỉnh)
⇒ΔAMB=ΔDMC(cmt)(đpcm).
b/ Ta có: ΔAMB=ΔDMC(cmt)
⇒^MAB=^MDC⇒^MAB=^MDC[ hai góc ở vị trí so le trong]
Vậy: AB // CD (đpcm).
Đúng 0
Bình luận (0)
cho tam giác ABC , M là trung điểm của BC . Trên tia AM lấy điểm D sao cho M là trung điểm của AD.a)chứng minh tam giác AMC tam giác DMB và BD // ACb)trên tia AB lấy điểm E sao cho B là trung điểm của AE . chứng minh tam giác ABC tam giác DCB và tam giác ABC tam giác BED.c)trên đường thẳng DE lấy điểm F sao cho D là tung điểm củaEF . chứng minh ba điểm A,C,F thẳng hàng và C là trung điểm của AF
Đọc tiếp
cho tam giác ABC , M là trung điểm của BC . Trên tia AM lấy điểm D sao cho M là trung điểm của AD.
a)chứng minh tam giác AMC = tam giác DMB và BD // AC
b)trên tia AB lấy điểm E sao cho B là trung điểm của AE . chứng minh tam giác ABC = tam giác DCB và tam giác ABC = tam giác BED.
c)trên đường thẳng DE lấy điểm F sao cho D là tung điểm của
EF . chứng minh ba điểm A,C,F thẳng hàng và C là trung điểm của AF
a) Xét ΔAMC và ΔDMB có
AM=DM(M là trung điểm của AD)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔAMC=ΔDMB(c-g-c)
⇒\(\widehat{CAM}=\widehat{BDM}\)(hai góc tương ứng)
mà \(\widehat{CAM}\) và \(\widehat{BDM}\) là hai góc ở vị trí so le trong
nên AC//BD(Dấu hiệu nhận biết hai đường thẳng song song)
b) Xét ΔAMB và ΔDMC có
AM=DM(M là trung điểm của AD)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)
⇒AB=CD(Hai cạnh tương ứng)
Ta có: ΔAMC=ΔDMB(cmt)
nên AC=BD(Hai cạnh tương ứng)
Xét ΔABC và ΔDCB có
AB=DC(cmt)
AC=DB(cmt)
BC chung
Do đó: ΔABC=ΔDCB(c-c-c)
Đúng 0
Bình luận (0)
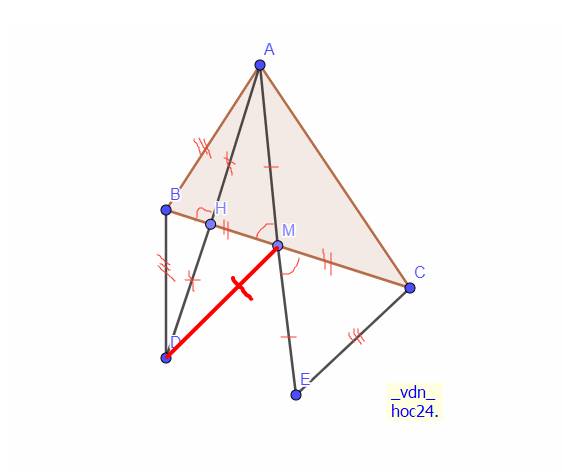
Cho tam giác ABC ( AB<AC), M là trung điểm cạnh BC. Trên tia AM lấy D sao cho M là trung điểm của AD. Vẽ AH vuông góc với BC tại H. Trên tia AH lấy điểm E sao cho H là trung điểm của AE. Chứng mình rằng:
a. BE vuông góc với CD
b.DE song song với BC
Cho tam giác abc nhọn (ab<ac).Kẻ ah vg góc với bc.Trên tia đối của tia ha lấy điểm m sao cho h là trung điểm của am.
a, c/m tam giác abh =tam giác mbh.
b, c/m bac=bmc.
c, gọi i là trung điểm của bc, trên tia đối của tia ia lấy điểm n sao cho i là trung điểmb của an.C/m nc=mb.
d, Cho ab= 13cm,ah=12cm,hc=16cm.tính ac,bc
a, xét tam giác ABH và tam giác MBH có : BH chung
góc AHB = góc MHB = 90
AH = HM do H là trđ của AM
=> tam giác ABH = tam giác MBH (2cgv)
b, tam giác ABH = tam giác MBH (câu a)
=> góc ABH góc MBH (đn)
và AB= BM (đn)
xét tam giác ABC và tam giác MBC có : BC chung
=> tam giác ABC = tam giác MBC (c-g-c)
=> góc BAC = góc BMC (đn)
c, xét tam giác BIA và tam giác CIN có :
góc BIA = góc CIN (đối đỉnh)
BI = IC do I là trđ của BC (gt)
AI = IN do I là trđ của AN (gt)
=> tam giác BIA = tam giác CIN (c-g-c)
=> AB = CN (đn)
AB = MB (Câu b)
=> CN = BM
d, dùng pytago thôi
Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.
a. Chứng minh: ΔAMB = ΔMCE
b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD
c. Tam giác AMD là tam giác gì? Vì sao?
\(\text{#TNam}\)
`a,` Xét Tam giác `AMB` và Tam giác `EMC` có:
`MA=ME (g``t)`
\(\widehat{AMB}=\widehat{CME} (\text {2 góc đối đỉnh})\)
`MB=MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác AMB = Tam giác EMC (c-g-c)}`
`b,` Vì Tam giác `AMB =` Tam giác `EMC (a)`
`-> AB = CE (\text {2 cạnh tương ứng}) (1)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`\text {BH chung}`
`=> \text {Tam giác ABH = Tam giác DBH (c-g-c)}`
`-> AB = BD (\text {2 cạnh tương ứng}) (2)`
Từ `(1)` và `(2) -> CE = BD.`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`\text {MH chung}`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HA = HD (g``t)`
`=> \text {Tam giác AMH = Tam giác DMH (c-g-c)}`
`-> MA = MD (\text {2 cạnh tương ứng})`
Xét Tam giác `AMD: MA = MD`
`-> \text {Tam giác AMD cân tại M}`
*Hoặc nếu như bạn có học rồi, thì mình có thể dùng cái này cũng được nè cậu:>.
Vì `MH` vừa là đường cao (hạ từ đỉnh `->` cạnh đối diện), vừa là đường trung tuyến.
Theo tính chất của tam giác cân `-> \text {Tam giác AMD là tam giác cân} (đpcm).`
Đúng 1
Bình luận (0)
a: Xét ΔAMB và ΔEMC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMAD cân tại M
Đúng 1
Bình luận (0)
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔMAB=ΔMEC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BA=BD=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trungtuyến
nên ΔMAD cân tại M
Đúng 0
Bình luận (0)
Cho tam giác ABC ( AB<AC), M là trung điểm cạnh BC. Trên tia AM lấy D sao cho M là trung điểm của AD. Vẽ AH vuông góc với BC tại H. Trên tia AH lấy điểm E sao cho H là trung điểm của AE. Chứng mình rằng:
a. BE vuông góc với CD
b.DE song song với BC
giúp với
Cho tam giác ABC vuông tại A.Gọi M và N thứ tự là trung điểm của BC và AC, trên tia AM lấy điểm D sao cho M là trung điểm của AD, trên tia BN lấy điểm E sao cho N là trung điểm của BE
a) Chứng minh tam giác ACM=tam giác DBM
b) Tính số đo của góc DBA
c) Chứng minh C là trung điểm của DE
Vẽ cả hình giúp mik nha!!!




