cho hình vuông tại m , đường cao mk . em viết biểu thức của các hệ thức đã học .
XT
Những câu hỏi liên quan
giúp em các cao thủ
Cho tam giác ABC vuông tại B , đường cao BH . Gọi M , N là hình chiếu của H trên AB , BC .
a) Viết các hệ thức lượng trong tam giác vuông AHB
b)Cho BC = 30cm , BH = 24cm ,Tính CH , AC , AH , AB .
c) Chứng minh : BN.BC + BM.BA = 2MN2
a: \(AB^2=HB^2+HA^2\)
\(BM\cdot BA=BH^2\)
\(AM\cdot AB=AH^2\)
\(BH\cdot HA=HM\cdot BA\)
\(HM^2=MA\cdot MB\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền BA, ta được:
\(BM\cdot BA=BH^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền BC, ta được:
\(BN\cdot BC=BH^2\)
Xét tứ giác BNHM có
\(\widehat{NBM}=\widehat{BNH}=\widehat{BMH}=90^0\)
Do đó: BNHM là hình chữ nhật
Suy ra: BH=NM
Ta có: \(BM\cdot BA+BN\cdot BC\)
\(=BH^2+BH^2\)
\(=2\cdot NM^2\)
Đúng 0
Bình luận (0)
Bạn tự vẽ hình nha.
a) \(sinA=\dfrac{BH}{AB},cosA=\dfrac{AH}{AB},tanA=\dfrac{BH}{AH},cotA=\dfrac{AH}{BH}\\sin \widehat{ABH}=\dfrac{AH}{AB},cos\widehat{ABH}=\dfrac{BH}{AB},tan\widehat{ABH}=\dfrac{AH}{BH},cot\widehat{ABH}=\dfrac{BH}{AH}\)
b)Áp dụng định lí Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(CH=\sqrt{BC^2-BH^2}=\sqrt{900-576}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(AC=\dfrac{BC^2}{HC}=\dfrac{900}{18}=50\left(cm\right)\)
\(AB=\dfrac{BH\cdot AC}{BC}=\dfrac{24\cdot50}{30}=40\left(cm\right)\)
\(AH=\dfrac{AB^2}{AC}=\dfrac{400}{50}=8\)(cm)
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
BN.BC=\(BH^2\)
BM.BA=\(BH^2\)
Suy ra, BN.BC+BM.BA=2\(BH^2\)
Xét tứ giác BMHN có:
góc BMH = góc MBN = góc HNB = \(90^0\)
nên tứ giác BMHN là hình chữ nhật.
suy ra BH = MN .
Suy ra, BN.BC+BM.BA = 2.\(MN^2\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH.
a) Hãy viết hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
b) Tính AH biết BH = 4cm; HC = 9cm
\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
Đúng 1
Bình luận (1)
Cho hình 36. Hãy viết hệ thức giữa:
Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
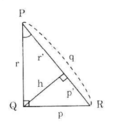
Hình 36
Cho tam giác IRS vuông tại I. Có IH là đường cao.
Câu 1: Viết 5 hệ thức về cạnh và đường cao trong tam giác vuông.
Câu 2: Biết hình chiếu của 2 cạnh góc vuông lần lượt là 9cm và 16cm.Tính các cạnh còn lại trong tam giác vuông đó.
Cho hình 36. Hãy viết hệ thức giữa:
Các cạnh góc vuông p, r và đường cao h.
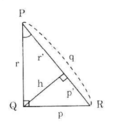
Hình 36
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
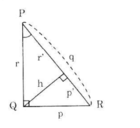
Hình 36
a) p 2 = p ' . q ; r 2 = r ' . q
![]()
c) h 2 = p ' . r '
Đúng 0
Bình luận (0)
Vẽ tam giác def vuông tại d có đường cao dh viết 4 hệ thức biểu thị nội dung các định lí về q.hệ giữa cạnh và đường cao trong tam giác
Xem chi tiết
Cho sin anpha = 0,6 . Hãy tính tan anphaVẽ tam giác def vuông tại d có đường cao dh viết 4 hệ thức biểu thị nội dung các định lí về q.hệ giữa cạnh và đường cao trong tam giácGiải tam giác vuông abc, vuông tại a. Biết ab=5cm, ac=12cm
Xem chi tiết
1. Ta có : sin2anpha + cos2anpha=1
=> (0.6)2 + cos2anpha =1
=> 0.36 + cos2anpha = 1
=> cos2anpha = 0.64
=>cos anpha =0.8
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tai A đường cao AH
A. Hãy viết hệ thức liên hệ giữa đường cao va hình chiếu của các cạch góc vuông trên canh huyền
B. Tinh AH biết BH=4cm HC=9cm
A. Hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền: \(AH^2=BH.CH\)
B. Ta có △ABC vuông tại A có đường cao AH\(\Rightarrow AH^2=BH.CH=4.9=36\Rightarrow AH=6\left(cm\right)\)
Đúng 1
Bình luận (0)




