Vẽ hình cho em với ạ .
Vẽ hình cho em với ạ .
TT
Những câu hỏi liên quan
cho hình vẽ biết BH = căn 2 cm, CH= căn 8 cm . tính diện tích tam giác ABC ( vẽ giúp em hình với ạ)(em đang cần gấp lắm ạ)
Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
viết chương trình vẽ hình chữ nhật với các kích thước được nhập vào từ bàn phím. Chương trình cho phép người đọc dùng vẽ nhiều hình chữ nhật cho đến khi người dùng không muốn vẽ nữa. Mn giúp em với ạ. Em cảm ơn ạ!!
Xem chi tiết
uses crt;
var a,b,i,j:integer;
st:string;
begin
clrscr;
repeat
write('Ban muon ve khong:'); readln(st);
if st='Yes' then
begin
write('Nhap chieu dai:'); readln(a);
write('Nhap chieu rong:'); readln(b);
for i:=1 to a do
begin
for j:=1 to b do
write('*');
writeln;
end;
end
else break;
until st='No'
readln;
end.
Đúng 1
Bình luận (0)
Cho em xin TÊN hình với ạ, nếu có bản vẽ các mặt thì cang tốt ạ !!!
Em cảm ơn nhiều ạ !!!

cho tia ox vẽ 2 tia oy và oz sao cho góc xoy = 110 độ , xoz = 150 độ .
tính yoz .![]() vẽ hình luôn ạ !
vẽ hình luôn ạ !
giúp em với mai em phải nộp rồi ạ
góc xOy<góc xOz
=>Oy nằm giữa Ox và Oz
=>góc xOy+góc yOz=góc xOz
=>góc yOz=40 độ
Đúng 0
Bình luận (0)
vẽ hình bông hoa trong scrath vẽ thế nào vậy ạ?cho em xin ý kiến với
vẽ giúp em hình Jeff The Killer với
Ai vừa ý em sẽ tick cho ạ
Em xin cảm ơn
Xem thêm câu trả lời
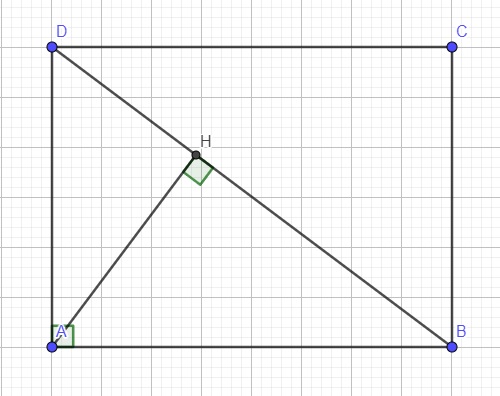
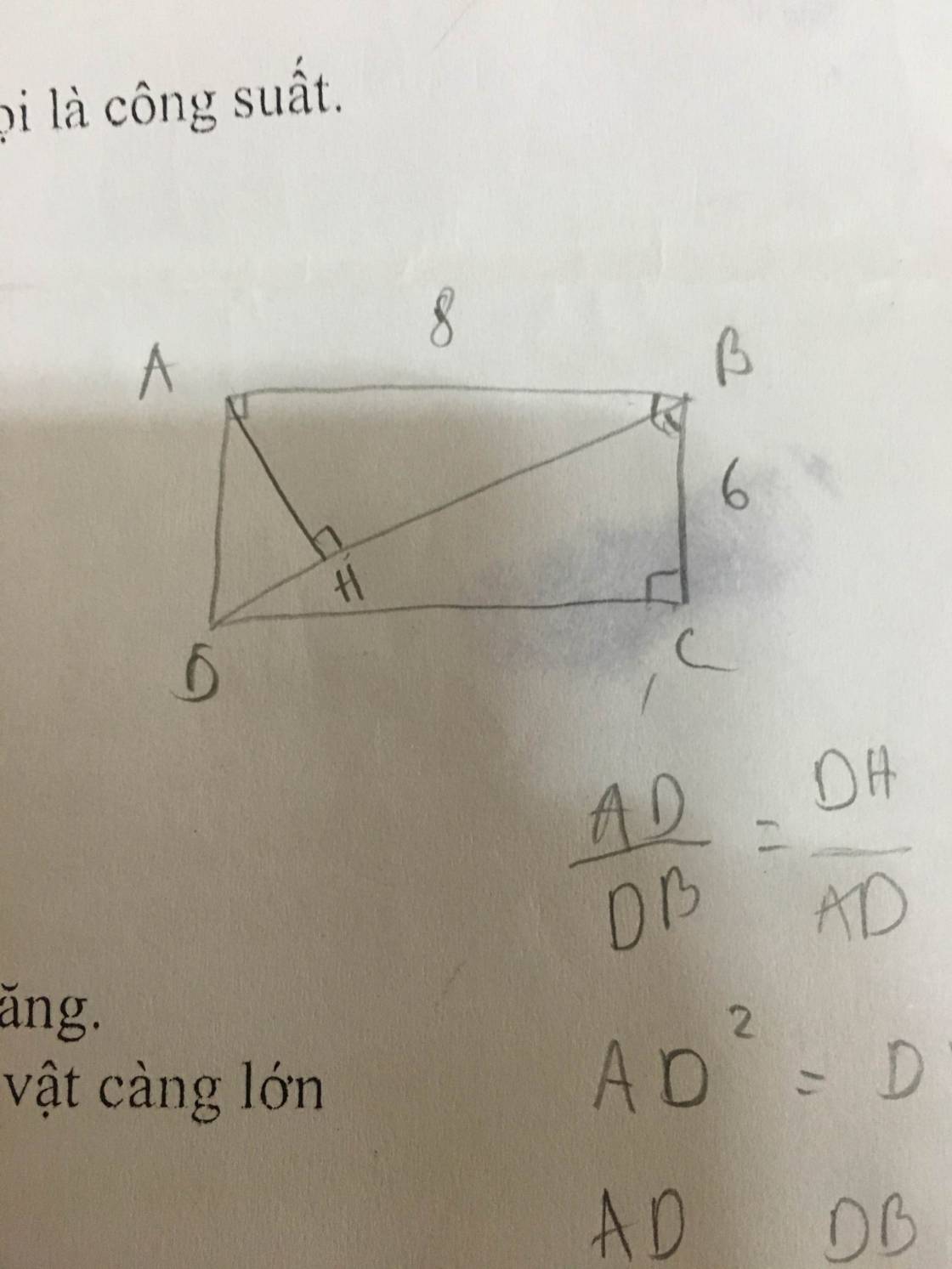
Mọi người giúp em làm bài toán hình này với ạ, kèm vẽ hình luôn nhé ạ. Em cảm ơn nhiều. - Cho hình chữ nhật ABCD có AB=8cm, BC= 6cm. Vẽ đường cao AH của tam giác ABD. a) chứng minh tam giác HBA đồng dạng với tam giác CDB b) Chứng minh: AD^2 = DH. DB c) Tính độ dài đoạn thẳng DH và AH
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm
Đúng 0
Bình luận (1)
mọi người giúp em với ạ, vẽ luôn hình ạ, em cảm ơn.
Giúp em bài 6 với 9 với ạ. Vẽ hình giúp en nx. Em cảm ơn ạ. 
Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)
Đúng 0
Bình luận (0)