a.
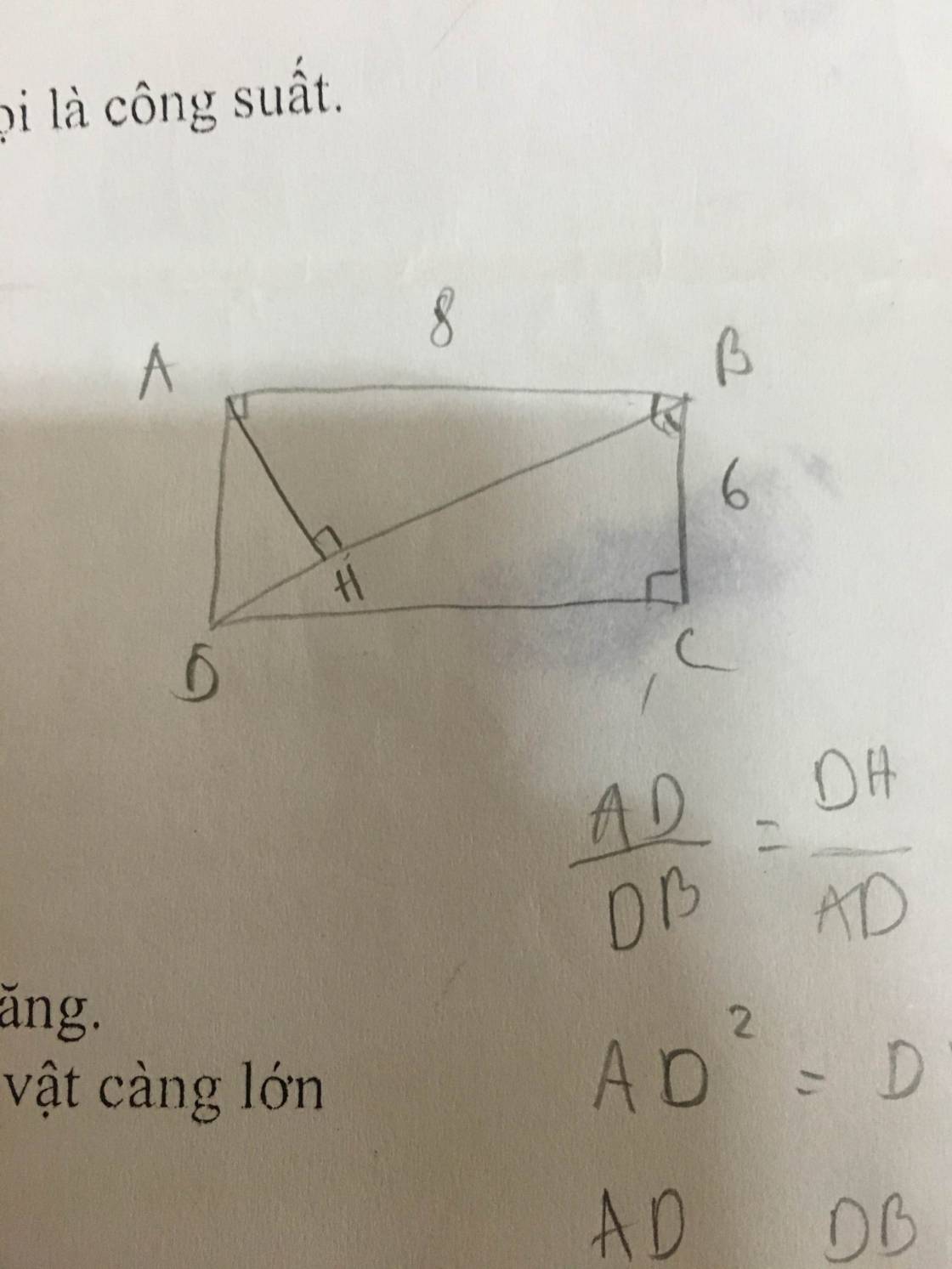
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
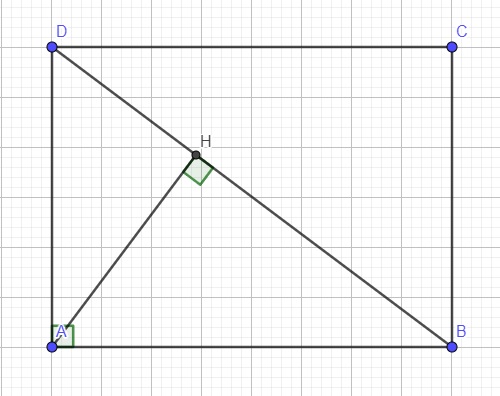
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm