Ta có:

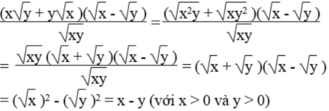
Vế trái bằng vế phải nên đẳng thức được chứng minh

trả lời hộ mình cái

b) Với x > 0; y > 0 ta có:

x + y x y - y x x y = x y x - y x y = x + y x - y = x - y

= ( x + y )( x  -  y ) = x - y

mình cũng cần

\(\begin{array}{l}T + H = 3{x^2}y - 2x{y^2} + xy + \left( { - 2{x^2}y + 3x{y^2} + 1} \right)\\ = 3{x^2}y - 2x{y^2} + xy - 2{x^2}y + 3x{y^2} + 1\\ = \left( {3{x^2}y - 2{x^2}y} \right) + \left( { - 2x{y^2} + 3x{y^2}} \right) + xy + 1\\ = {x^2}y + x{y^2} + xy + 1\\T - H = 3{x^2}y - 2x{y^2} + xy - \left( { - 2{x^2}y + 3x{y^2} + 1} \right)\\ = 3{x^2}y - 2x{y^2} + xy + 2{x^2}y - 3x{y^2} - 1\\ = \left( {3{x^2}y + 2{x^2}y} \right) + \left( { - 2x{y^2} - 3x{y^2}} \right) + xy - 1\\ = 5{x^2}y - 5x{y^2} + xy - 1\end{array}\)

Chọn B.

1) Ta có: \(\dfrac{1}{7}x^2y^3\cdot\left(-\dfrac{14}{3}xy^2\right)\cdot\left(-\dfrac{1}{2}xy\right)\left(x^2y^4\right)\)

\(=\left(-\dfrac{1}{7}\cdot\dfrac{14}{3}\cdot\dfrac{-1}{2}\right)\left(x^2y^3\cdot xy^2\cdot xy\cdot x^2y^4\right)\)

\(=\dfrac{1}{3}x^6y^{10}\)

2) Ta có: \(\left(3xy\right)^2\cdot\left(-\dfrac{1}{2}x^3y^2\right)\)

\(=9xy^2\cdot\dfrac{-1}{2}x^3y^2\)

\(=-\dfrac{9}{2}x^4y^4\)

3) Ta có: \(\left(-\dfrac{1}{4}x^2y\right)^2\cdot\left(\dfrac{2}{3}xy^4\right)^3\)

\(=\dfrac{1}{16}x^4y^2\cdot\dfrac{8}{27}x^3y^{12}\)

\(=\dfrac{1}{54}x^7y^{14}\)