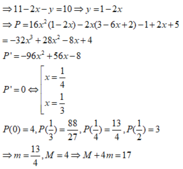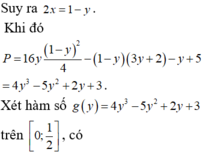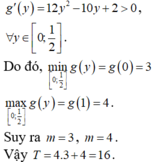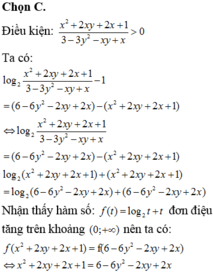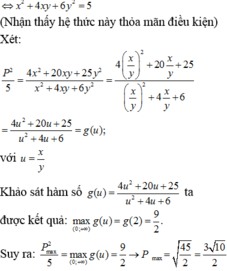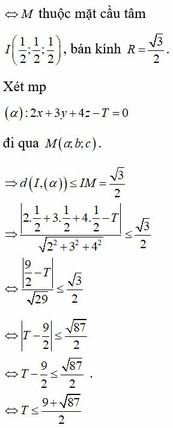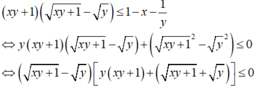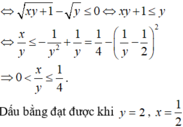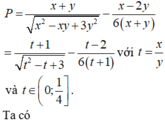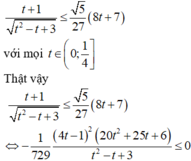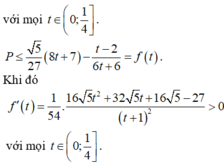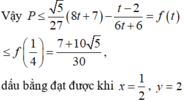cho hai số thực x,y thỏa mãn 2x+3y\(\le7\). Giá trị lớn nhất của biểu thức P=x+y+xy là
AN
Những câu hỏi liên quan
cho các số thực dương x,y thỏa mãn \(\sqrt{y}\left(y+1\right)-6x-9=\left(2x+4\right)\sqrt{2x+3}-3y\). Tìm giá trị lớn nhất của biểu thức M = xy + 3y - 4\(x^2\) - 3
Đặt \(\left\{{}\begin{matrix}\sqrt{2x+3}=a\ge0\\\sqrt{y}=b\ge0\end{matrix}\right.\)
\(\Rightarrow b\left(b^2+1\right)-3a^2=\left(a^2+1\right)a-3b^2\)
\(\Rightarrow a^3-b^3+3a^2-3b^2+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+\left(a-b\right)\left(3a+3b\right)+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+3a+3b+1\right)=0\)
\(\Leftrightarrow a=b\Rightarrow\sqrt{2x+3}=\sqrt{y}\)
\(\Rightarrow y=2x+3\)
\(\Rightarrow M=x\left(2x+3\right)+3\left(2x+3\right)-4x^2-3\) tới đây chắc chỉ cần bấm máy
Đúng 0
Bình luận (0)
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
cho x,y là hai số thực dương thỏa mãn x+y≤xy.Tìm giá trị lớn nhất của biểu thức M=\(\dfrac{1}{2x^2+3y^2}+\dfrac{1}{3x^2+2y^2}\)
\(x+y\le xy\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}\le1\)
\(M=\dfrac{1}{2\left(x^2+y^2\right)+y^2}+\dfrac{1}{2\left(x^2+y^2\right)+x^2}\le\dfrac{1}{4xy+y^2}+\dfrac{1}{4xy+x^2}\)
\(B\le\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{y^2}\right)+\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{x^2}\right)=\dfrac{1}{25}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{2}{xy}+\dfrac{6}{xy}\right)\)
\(M\le\dfrac{1}{25}\left[\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{3}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right]=\dfrac{1}{10}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le\dfrac{1}{10}\)
\(M_{max}=\dfrac{1}{10}\) khi \(x=y=2\)
Đúng 2
Bình luận (2)
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
2
, và
log
(
11
-
2
x
-
y
)
2...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hai số thực x, y dương thỏa mãn:
log
2
x
2
+
2
x
y
+
2
x
+
1
3
-
3
y
2...
Đọc tiếp
Cho hai số thực x, y dương thỏa mãn: log 2 x 2 + 2 x y + 2 x + 1 3 - 3 y 2 - x y + x = 6 - x 2 - 4 x y - 6 y 2 Giá trị lớn nhất của biểu thức P=2x+5y bằng
![]()
![]()
![]()
Cho x,y là hai số thực dương thỏa. mãn x+y=5 Giá trị nhỏ nhất của biểu thức P=\(\dfrac{4x+y}{xy}-\dfrac{2x-y}{4}\)
Bạn kiểm tra lại đề bài, với biểu thức thế này thì không thể tìm được điểm rơi (nó là nghiệm của 1 pt bậc 4 hệ số rất xấu ko thể giải được)
Đúng 0
Bình luận (0)
Cho x, y, z là các số thực thỏa mãn điều kiện
4
x
+
9
y
+
16
z
2
x
+
3
y
+
4
z
. Tìm giá trị lớn nhất của biểu thức
T
2
x
+
1
+...
Đọc tiếp
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
A. 13 + 87 2
B. 11 + 87 2
C. 7 + 37 2
D. 9 + 87 2
Cho x, y, z là các số thực thỏa mãn điều kiện
4
x
+
9
y
+
16
z
2
x
+
3
y
+
4
z
. Tìm giá trị lớn nhất của biểu thức
T
...
Đọc tiếp
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
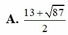
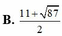
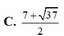
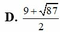
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện
(
x
y
+
1
)
(
x
y
+
1
-
y
)
≤
1
-
x
-
1
y
. Tìm giá trị lớn nhấ...
Đọc tiếp
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện ( x y + 1 ) ( x y + 1 - y ) ≤ 1 - x - 1 y . Tìm giá trị lớn nhất của biểu thức P = x + y x 2 - x y + 3 y 2 - x - 2 y 6 ( x + y )
A. 5 3 - 7 30
B. 7 30 - 5 3
C. 5 3 + 7 30
D. 5 + 7 30