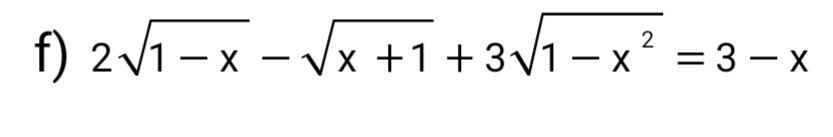 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs
TN
Những câu hỏi liên quan
Mn chỉ mik vs
Giải hệ pt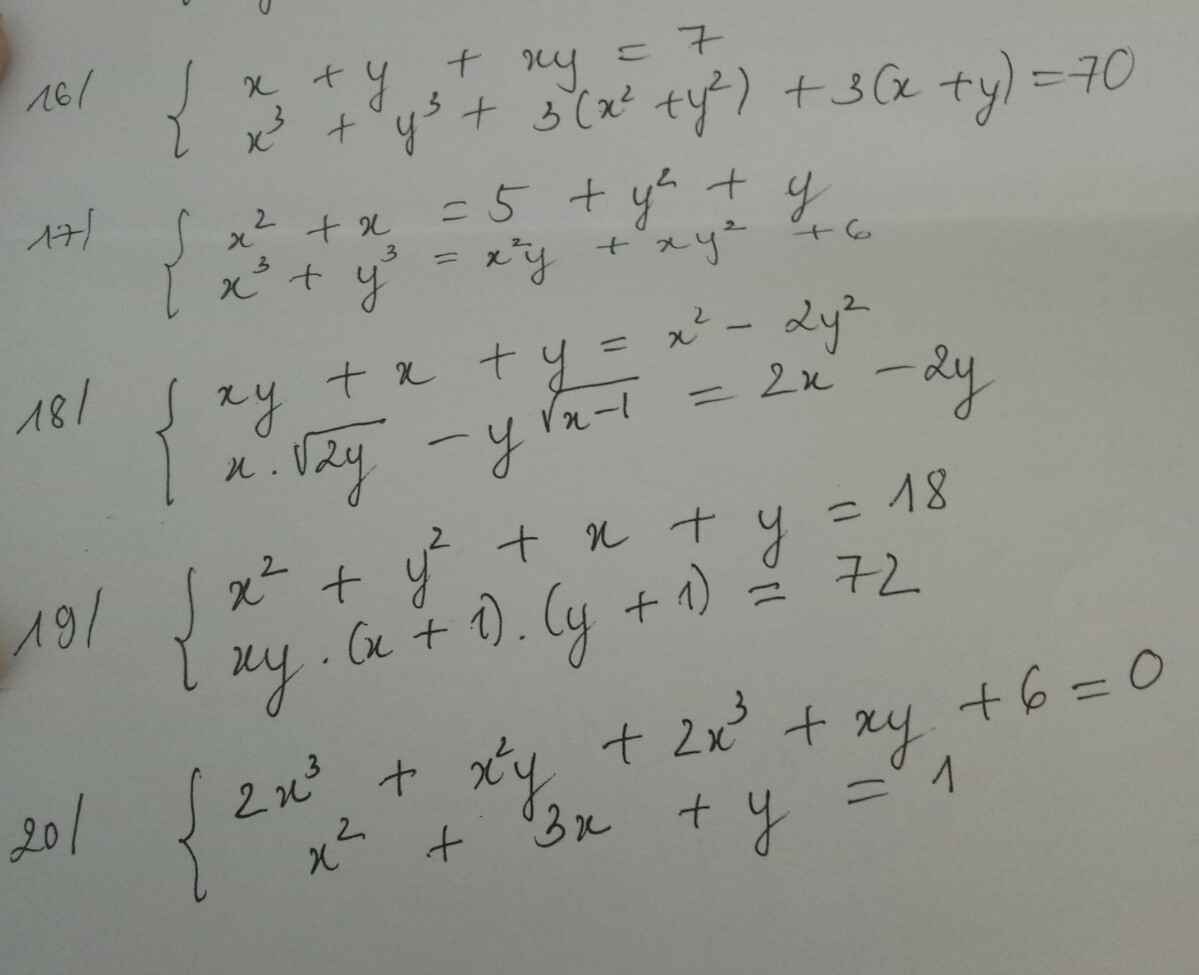
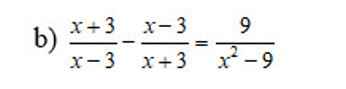
giải giúp pt này vs mn
\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)
Đúng 4
Bình luận (0)
Giải pt :
x/40 - x/50 = 1/3
giải hộ mik vs
MIK ĐANG VỘI LẮM! GIÚP MIK VS
Bài này quá dễ
x/40 - x/50= 1/3
<=>5x/200 - 4x/200=1/3
<=> x/200= 1/3
<=> x= 200/3.
Đúng 0
Bình luận (0)
bạn ê, mik bị ngu toán, lười suy nghĩ ấy mà nên đừng nói dễ hay khó j vs mik
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
MN ơi giúp mik vs mai mik thi í bạn nào biết giải giúp mik vs ạ :((
mn giúp em vs:
(x+1) mũ 4 + (x+3) mũ 4=2m
a, giải pt vs m=1
b, tìm m để pt có 2 no pb
a) \(\left(x+1\right)^4+\left(x+3\right)^4=2m\left(1\right)\)
Đặt \(x+2=t\)
Khi đó phương trình \(\left(1\right)\) trở thành \(\left(t-1\right)^4+\left(t+1\right)^4=2m\)
\(\Leftrightarrow2t^4+12t^2-2m+2=0\)
\(\Leftrightarrow t^4+6t^2-m+1=0\left(2\right)\)
Đặt \(t^2=u\left(u\ge0\right)\)
Khi đó phương trình \(\left(2\right)\) trở thành \(u^2+6u-m+1=0\left(3\right)\)
Thay \(m=1\) vào \(\left(3\right)\) ta có:
\(u^2+6u-1+1=0\Leftrightarrow u^2+6u=0\Leftrightarrow u\left(u+6\right)=0\Leftrightarrow\left[{}\begin{matrix}u=0\\u+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}u=0\left(\text{nhận}\right)\\y=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow x+2=0\Leftrightarrow x=-2\)
Vậy với \(m=1\) thì phương trình có nghiệm là \(x=-2\).
b) Để phương trình có hai nghiệm phân biệt thì \(\left(3\right)\) trái dấu \(\Leftrightarrow-m+1< 0\Leftrightarrow m>1\)
Vậy với \(m>1\) thì phương trình có hai nghiệm phân biệt.
Đúng 2
Bình luận (0)
Giải giúp mik bài này bằng cách lập pt vs ạ 
bạn chịu khó đánh máy ra đc không? Chứ khó nhìn đề lắm
Đúng 1
Bình luận (0)
giải chi tiết giúp mik nha, vt hẳn pt ra vs ạ

Giải giúp mik vs mn
Mn giải giúp mik vs 
Câu 1 :
\(a,5\left(x+2\right)=2\left(x-4\right)\)
\(\Leftrightarrow5x+10=2x-8\)
\(\Leftrightarrow5x-2x=-8-10\)
\(\Leftrightarrow3x=-18\)
\(\Leftrightarrow x=-6\)
\(b,x\left(x+2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{3;2\right\}\)
\(c,\dfrac{2x-5}{4}-\dfrac{x+1}{3}=\dfrac{1}{2}\)
\(\Leftrightarrow3\left(2x-5\right)-4\left(x+1\right)=6\)
\(\Leftrightarrow6x-15-4x-4=6\)
\(\Leftrightarrow6x-4x=6+4+15\)
\(\Leftrightarrow2x=25\)
\(\Leftrightarrow x=\dfrac{25}{2}\)
Vậy \(S=\left\{\dfrac{25}{2}\right\}\)
\(d,\dfrac{3}{x-2}-\dfrac{6}{x+2}=\dfrac{-x}{x^2-4}\left(đkxđ:x\ne\pm2\right)\)
\(\Leftrightarrow3\left(x+2\right)-6\left(x-2\right)=-x\)
\(\Leftrightarrow3x+6-6x+12=-x\)
\(\Leftrightarrow3x-6x+x=-12-6\)
\(\Leftrightarrow-2x=-18\)
\(\Leftrightarrow x=9\left(nhận\right)\)
Vậy \(S=\left\{9\right\}\)
Đúng 2
Bình luận (0)
Câu 3 :
a, Xét ΔABD và ΔHBA có :
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABD\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔADH và ΔDBC có :
\(\widehat{H}=\widehat{C}=90^0\)
\(\widehat{ADH}=\widehat{DBC}\left(AB//CD,slt\right)\)
\(\Rightarrow\Delta ADH\sim\Delta DBC\)
c, Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
\(\Rightarrow AB^2=BH.BD\)
d, Xét ΔABD vuông ở A , theo định lý Pi-ta-go ta được :
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{12^2+9^2}=15\left(cm\right)\)
Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
hay \(\dfrac{12}{BH}=\dfrac{15}{12}\)
\(\Rightarrow BH=\dfrac{12.12}{15}=9,6\left(cm\right)\)
Đúng 1
Bình luận (0)





