Cho \(\Delta\)ABC \(⊥\)A,AC = 20 cm.Kẻ AH \(⊥\)BC.Biết BH = 9 cm ,HC = 16 cm.Tính AB,AH
NT
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A,AC =20 cm.Kẻ AH\(⊥\)BC.Biết BH = 9 cm.HC = 16 cm.Tính AB,AH.
Xét \(\Delta HAC\)Ta có : \(HA^2-HC^2=AC^2\)
Hay \(HA^2+16^2=20^2\)
\(HA^2=20^2-16^2=144\)
\(\Rightarrow\)\(HA=12\)
Xét \(\Delta ABH\)
\(HA^2+HB^2=BA^2\)
Hay :\(9^2+12^2=BA^2\)
\(BA^2=225\)
\(\Rightarrow BA=15\)
Vậy AH = 12cm : AB = 15cm
Bạn tự vẽ hình được không ? mình không biết vẽ trên Onlinemath
Đúng 0
Bình luận (0)
mk bảo nè mk nk này vs nk Noo Phước Thịnh là 1 người đó mk gửi câu hỏi để trả lời mà ko hiểu sao trả lời mấy lần rùi mà vẫ ko đc
Đúng 0
Bình luận (0)
bài 1: cho ABC vuông tại A có AB<AC. Kể AH song song BC(HE,BC) cho biết AH=12 cm,BH=9 cm,AC=20 cm.Tính độ dài AB và HC
cho tam giác ABC vuông tại A;đường cao AH
Biết BH=9 cm,HC=16 cm.tính AH=? cm
cứu tao với nếu đúng tao tick
Ta có CA^2=CH^2+HA^2 Định lí pytago
AB^2=BH^2+HA^2 Định lí Pytago
=> CA^2+AB^2=CH^2+HA^2+HB^2+HA^2=36+2HA^2+81=CB^2=(6+9)^2=225
2HA^2=225-36-81=108
HA^2=54
=> HA=\(3\sqrt{6}cm\) nha bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác vuông tại a có ac = 20 cm kẻ ah vuông góc bc tại h biết bh= 9 cm ,hc= 16 cm . tính ab , ah ?
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=AC^2-HC^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm
Đúng 2
Bình luận (0)
Vì AH⊥BC => △ABH và △ACH vuông tại H Áp dụng định lý Pi-ta-go vào △ABH và △ACH, ta có:
AC2=AH2+CH2
=>AH2=AC2-CH2
AH2=202- 162
AH2= 144 => AH= căn bậc hai của 144= 12 (cm)
AB2=AH2+BH2
AB2= 122+92
AB2= 144+81
AB2= 225 => AB= căn bậc hai của 225 =15 (cm)
Vậy AB = 15 cm, AH = 12 cm
Đúng 1
Bình luận (0)
cho tam giác ABC vuông ở A có AC=20cm,kẻ AH vuông góc với BC.Biết BH=9CM,HC=16CM.Tính AB,AH
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
Đúng 2
Bình luận (1)
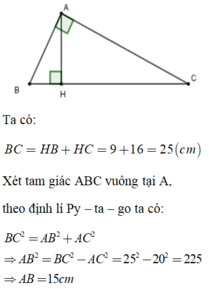
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
Đúng 2
Bình luận (1)
Ta có :
BC = BH + HC
=> BC = 9 + 16
=> BC = 25 (cm)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+BC^2\) (định lí Py - ta - go)
=> \(25^2=AB^2+20^2\)
=> \(AB^2=225\)
=> AB = 15 (cm)
Xét Δ ABH vuông tại H, có :
\(AB^2=BH^2+AH^2\) (định lí Py - ta - go)
=> \(15^2=9^2+AH^2\)
=> \(AH^2=144\)
=> AH = 12 (cm)
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có AC 20 cm. Kẻ AH vuông góc với BC. Biết BH 9cm, HC 16 cm. Tính độ dài cạnh AB, AH? A.
A
H
12
c
m
;
A
B
15
c
m
B.
A
H
10
c
m
;
A
B
15
c
m
C.
A
H
15
c
m
;
A...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 20 cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16 cm. Tính độ dài cạnh AB, AH?
A. A H = 12 c m ; A B = 15 c m
B. A H = 10 c m ; A B = 15 c m
C. A H = 15 c m ; A B = 12 c m
D. A H = 12 c m ; A B = 13 c m
cho ABC vuông tại A có AB=30cm.Kẻ AH vuông góc với BC.Biết AH=24cm,BC=50cm.Tính độ dài cạnh AC,BH và HC?
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=50^2-30^2=1600\)
=>AC=40(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(BH=\dfrac{30^2}{50}=18\left(cm\right);CH=\dfrac{40^2}{50}=32\left(cm\right)\)
Đúng 3
Bình luận (0)
Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=50^2-30^2=1600\Rightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABH\) vuông tại H ta có: \(AH^2+BH^2=AB^2\Rightarrow24^2+BH^2=30^2\Rightarrow BH^2=30^2-24^2=324\Rightarrow BH=\sqrt{324}=18\left(cm\right)\)\(HC=BC-BH=50-18=32\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A có AC =20 cm kẻ AH vuông goc BC. biết BH=9 cm, HC=16cm. Tính AB,AH
vì BH=9 , HC=16
=> BC=25
xét tam giác ABC ...., ta có
BC^2=CA^2+AB^2
hay 25^2=20^2 +Ab^2
625=400 + AB^2
AB^2=225
AB=15
xét tam giác ABH...., ta có
AB^2=AH^2 + BH^2
hay 15^2= Ah^2 + 9^2
225= AH^2 +81
AH^2= 144
AH=12
thêm kl và những chỗ còn thiếu vào nhé
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AC =20 cm kẻ AH vuông goc BC. biết BH=9 cm, HC=16cm. Tính AB,AH

Ta có: \(BC=BH+CH=9+16=25\)
Áp dụng định lý Py- ta - go vào \(\Delta ABC\), ta được:
\(AB^2=BC^2-AC^2\)
\(\Leftrightarrow AB^2=25^2-20^2\)
\(\Leftrightarrow AB^2=625-400\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=\sqrt{225}=15\)
Áp dụng định lý Py- ta - go vào \(\Delta AHC\), ta được:
\(AH^2=AC^2-CH^2\)
\(\Leftrightarrow AH^2=20^2-16^2\)
\(\Leftrightarrow AH^2=400-256\)
\(\Leftrightarrow AH^2=144\)
\(\Leftrightarrow AH=\sqrt{144}=12\)
Đúng 0
Bình luận (0)
Bài làm
BC=BH+HC=9+6=25(cm)BC=BH+HC=9+6=25(cm)
Áp dụng định lý Py-ta-go với tam giác ABC vuông tại A, ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇒AB2=BC2+AC2=252−202⇒AB2=BC2+AC2=252−202
=625−400=225=152=625−400=225=152
Vậy AB=15cm
Áp dụng định lý Py-ta-go với tam giác AHC vuông tại H, ta có:
AH2=AC2−HC2=202−162=122AH2=AC2−HC2=202−162=122
Vậy AH= 12cm
# Học tốt #
Đúng 0
Bình luận (0)
Bài làm
~ Vừa rồi mik viết thiếu mũ nhá. ~
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Tam giác ABC vuông tại A nên :
BC2 = AB2 + AC2
252 = AB2 + 162
=> AB2 = 252 - 202
AB2 = 625 - 400 = 225 = 152
=> AB = 15 (cm)
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = AH2 + 162
=> AH2 = 202 - 162
AH = 400 - 256 = 144 = 122
=> AH = 12 (cm)
Vậy AB = 15 cm ; AH = 12 cm
# Học tốt #
Đúng 0
Bình luận (0)
Xem thêm câu trả lời