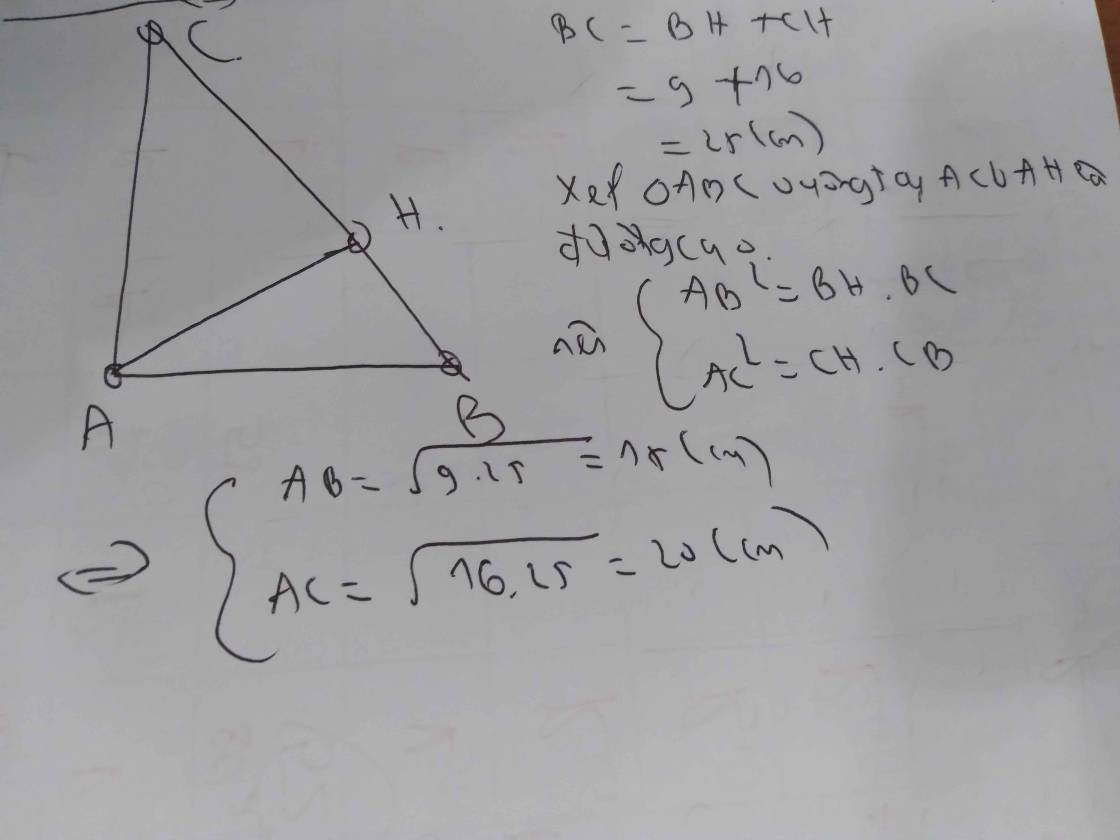
Cho tam giác ABC vuông tại A,AC =20 cm.Kẻ AH\(⊥\)BC.Biết BH = 9 cm.HC = 16 cm.Tính AB,AH.
LH
Những câu hỏi liên quan
Cho \(\Delta\)ABC \(⊥\)A,AC = 20 cm.Kẻ AH \(⊥\)BC.Biết BH = 9 cm ,HC = 16 cm.Tính AB,AH
Độ dài cạnh BC là :
9 + 16 = 25 ( cm )
Có tam giác ABC vuông tại A
=> Áp dụng theo định lý Pi - ta - go ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=25^2-20^2\)
\(\Rightarrow AB^2=225\)
\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)
Có AH vuông góc vs BC
Áp dụng theo định lý Py - ta - go ta có:
\(AB^2=AH^2+HB^2\)
\(\Rightarrow AH^2=AB^2-HB^2\)
\(\Rightarrow AH^2=15^2-9^2\)
\(\Rightarrow AH^2=144\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)
Đúng 0
Bình luận (0)
BC = ?
BC - BH + CH
Mà BH = 9N cm ( gt ) ; CH = 16 cm ( gt )
\(\Rightarrow\)BC = 9 + 16
BC = 25 cm
AB = ?
Vì \(\Delta\)ABC \(⊥\)tại A
Áp dụng định lí pi - ta - go, ta có :
AB2 = BC2 - AC2
Mà BC = 25 cm ; AC = 20 cm ( gt )
\(\Rightarrow\)AB2 = 252 - 202
AB2 = 225
AB = 15 cm
AH = ?
Vì \(\Delta\)ABH\(⊥\)tại H
Áp dụng định lí Pi - ta - go , ta có :
AH2 = AB2 - BH2
Mà AB = 15 cm ( cmt ); BH = 9 cm ( gt )
\(\Rightarrow\)AH2 = 152 - 92
AH2 = 144
AH = 12 cm
Đúng 0
Bình luận (0)
Bài 1:Cho tam giác ABC vuông tại A,đường cao AH.Biết AB=15,AC=20,tính các đoạn thẳng AH,BH,CH,BC
Bài 2:Cho tam giác ABC vuông tại A,đường cao AH=12,cạnh huyền BC=25
a)tính BH
b)Tính AB,AC
Bài 3:Cho tam giác ABC,đường cao AH \(\perp\)BC.Biết AB=6,CH=6,4
a)Tính BH
b)Tính AC.
Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
bạn cho mình hỏi tại sao AH2 =BH.HC??
Xem thêm câu trả lời
cho tam giác ABC vuông tại A vẽ đường cao AH,H thuốc BC.biết AB=6cm,AC= 8cm a. chứng minh tam giác HBA đồng dạng với với tam giác ABC b. tính BC,AH,BH c. kẻ HI vuông góc với AC tại I chứng minh HC^2=IC*AC
a, Xét tam giác HBA và tam giác ABC có
^B _ chung ; ^BHA = ^BAC = 900
Vậy tam giác HBA ~ tam giác ABC (g.g)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}cm\)
\(\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
b, Xét tam giác CHI và tan giác CAH có
^AIH = ^CHA = 900
^C _ chung
Vậy tam giác CHI ~ tam giác CAH (g.g)
\(\dfrac{CH}{AC}=\dfrac{CI}{CH}\Rightarrow CH^2=CI.AC\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông ở A có AC=20cm,kẻ AH vuông góc với BC.Biết BH=9CM,HC=16CM.Tính AB,AH
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
Đúng 2
Bình luận (1)
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
Đúng 2
Bình luận (1)
Ta có :
BC = BH + HC
=> BC = 9 + 16
=> BC = 25 (cm)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+BC^2\) (định lí Py - ta - go)
=> \(25^2=AB^2+20^2\)
=> \(AB^2=225\)
=> AB = 15 (cm)
Xét Δ ABH vuông tại H, có :
\(AB^2=BH^2+AH^2\) (định lí Py - ta - go)
=> \(15^2=9^2+AH^2\)
=> \(AH^2=144\)
=> AH = 12 (cm)
Đúng 1
Bình luận (1)
1. Cho tam giác ABC vuông tại A, biết AH 16, BH 9. Tính AB.2. Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Tính độ dài HB.3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12, BC 15. Tính HC.4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 6, HC 9. Tính độ dài AC.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, BC 16cm. Tính AH6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 8cm, HC 12 cm. Tính AC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (3)
cho tam giác ABC vuông tại A có AC=20cm.Kẻ AH vuông góc với BC.Biết BH=9cm,HC=16cm.Tính độ các cạnh góc vuông AB và AC
help meee
cho tam giác abc vuông tại a
a) biết bc=20 cm; 4ab=3ac tính ab, ac
b) kẻ ah vuông góc với bc và ac=20 cm; bh=9 cm ch=16 cm tính ab, ah
a, Ta có : 4AB = 3CA => AB /3 = AC /4 => AB^2/9 = AC^2/16
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}=\dfrac{400}{25}=16\Rightarrow AB=12cm;AC=16cm\)
b, Ta có : BH + CH = BC = 25 cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=15cm\)
Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-HB^2}=12cm\)
Đúng 2
Bình luận (0)
bài 1: cho ABC vuông tại A có AB<AC. Kể AH song song BC(HE,BC) cho biết AH=12 cm,BH=9 cm,AC=20 cm.Tính độ dài AB và HC
cho tam giác vuông tại a có ac = 20 cm kẻ ah vuông góc bc tại h biết bh= 9 cm ,hc= 16 cm . tính ab , ah ?
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=AC^2-HC^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm
Đúng 2
Bình luận (0)
Vì AH⊥BC => △ABH và △ACH vuông tại H Áp dụng định lý Pi-ta-go vào △ABH và △ACH, ta có:
AC2=AH2+CH2
=>AH2=AC2-CH2
AH2=202- 162
AH2= 144 => AH= căn bậc hai của 144= 12 (cm)
AB2=AH2+BH2
AB2= 122+92
AB2= 144+81
AB2= 225 => AB= căn bậc hai của 225 =15 (cm)
Vậy AB = 15 cm, AH = 12 cm
Đúng 1
Bình luận (0)