Cho △ABC nhọn cs đường cao BD và CE
hãy chứng minh BD.AC = CE.AB
giúp zới nha
TT
Những câu hỏi liên quan
Cho tam giác ABC nhọn nối tiếp đường tròn (O) các đường cao BD và CE của tam giác ABC cắt nhau tại H chứng minh a) tứ giác AEHD nội tiếp đuong tròn b) cung AED_|_ACB c) OA_|_ED giúp tui zới
Cho tam giác ABC nhọn, các đường cao BD và CE. Chứng minh góc ABC = góc ADE cắt đường cao BD và CE Bạn nào giải nhanh giúp mk với nha, mk đang gấp
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN MD.MB
Đọc tiếp
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
Cho tam giác ABC nhọn và nội tiếp đường tròn O. Hai đường cao BE, CF của tam giác ABC cắt đường tròn O lần lượt tại K và I. a) Chứng minh EF // IK. b) IK cắt AB và AC lần lượt tại P và Q. Chứng minh OA⊥PQ . c) Tia AO cắt (O) tại D, BE và CF cắt nhau tại H. Chứng minh tứ giác BHCD là hình bình hành. d) Tia AH cắt (O) tại M. Chứng minh AB.DC = MB.AC. e) Chứng minh BD.AC + CD.AB = AD.BC.
Cho tam giác ABC nhọn và nội tiếp đường tròn O. Hai đường cao BE, CF của tam giác ABC cắt đường tròn O lần lượt tại K và I. a) Chứng minh EF // IK. b) IK cắt AB và AC lần lượt tại P và Q. Chứng minh OA⊥PQ . c) Tia AO cắt (O) tại D, BE và CF cắt nhau tại H. Chứng minh tứ giác BHCD là hình bình hành. d) Tia AH cắt (O) tại M. Chứng minh AB.DC = MB.AC. e) Chứng minh BD.AC + CD.AB = AD.BC.
cho tam giác abc nhọn đường cao bd ce chứng minh rằng Sbcde = Sabc.Sin^2 a
cho tam giác abc nhọn đường cao bd ce chứng minh rằng Sbcde = Sabc.Sin^2 a
Cho tam giác nhọn ABC, hai đường cao BD và CE. Chứng minh S A D E = S A B C . cos 2 A
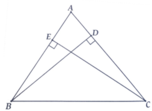
Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có hai đường cao BD và CE.
a) Chứng minh ADBAEC.
b) Gọi H là giao điểm của BD và CE . Chứng minh HE.HC HD.HB
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, các đường cao BD và CE. Bẽ BM vuông góc với DE tại M, CN vuông góc với DE tại N. Chứng minh ME=ND.
Giúp mik nha!!!
\(\triangle BEC \) vuông tại E có: \(EB^2+EC^2=BC^2\qquad (1)\) (định lý Pythagoras)
Tương tự như trên, ta có:
\(BD^2+DC^2=BC^2\qquad (2)\),
\(BD^2+DC^2=BD^2\qquad (3 )\),
\(DN^2+NC^2=DC^2\qquad(4)\),
\(EM^2+MB^2=BE^2\qquad(5)\),
\(EN^2+NC^2=EC^2\qquad(6)\).
Từ \((1)\) và \((2)\), suy ra: \(BE^2+EC^2=BD^2+DC^2(=BC^2)\).
Thay \((3)\), \((4)\), \((5)\) và \((6)\) vào đẳng thức trên, ta được:
\((ME^2+MB^2)+(EN^2+NC^2)=(DM^2+MB^2)+(DN^2+NC^2)\\ \Leftrightarrow ME^2+EN^2=MD^2+DN^2\\ \Leftrightarrow ME^2+(ED+DN)^2=(ME+ED)^2+DN^2\\ \Leftrightarrow ME^2+ED^2+2ED\cdot DN+DN^2=ME^2+2ME\cdot ED+ED^2+DN^2\\ \Leftrightarrow 2DE\cdot DN=2ME\cdot ED \Leftrightarrow DN=ME \space\text{(đpcm)}\)