S ABC=1/2*BD*AC=1/2*CE*AB
=>BD*AC=CE*AB
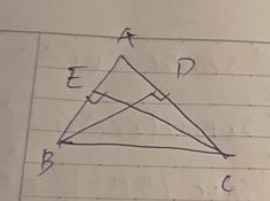
Có: \(S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}CE.AB\)
\(\Rightarrow BD.AC=CE.AB\) (đpcm)
S ABC=1/2*BD*AC=1/2*CE*AB
=>BD*AC=CE*AB

Có: \(S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}CE.AB\)
\(\Rightarrow BD.AC=CE.AB\) (đpcm)
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
Cho tam giác ABC nhọn có hai đường cao BD và CE.
a) Chứng minh ADBAEC.
b) Gọi H là giao điểm của BD và CE . Chứng minh HE.HC HD.HB
Cho tam giác nhọn ABC, các đường cao BD và CE. Bẽ BM vuông góc với DE tại M, CN vuông góc với DE tại N. Chứng minh ME=ND.
Giúp mik nha!!!
cho tam giác ABC nhọn, BD là đường trung tuyến, CE là đường cao. Sao cho BD = CE và góc BDC = góc ECA. BD cắt CE tại H. Chứng minh a) HE*HC = HB*HD
b) chứng minh tam giác ABC đều
Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh
B C 2 = B H . B D + C H . C E .
Cho ΔABC nhọn. Các đường cao AH và BD cắt nhau tại E.
a, Chứng minh: ΔAHC ~ ΔBDC
Vẽ hộ mình hình nữa nha
Cho tam giác nhọn ABC có 2 đường cao BD và CE. Chứng minh \(\Delta ADE~\Delta ABC\)
Cho tam giác nhọn ABC các đường cao BD CE cắt nhau ở H chứng minh rằng. a. tam giác AEC đồng dạng tam giác ADB b. Kẻ HK vuông góc với BC ( k thuộc BC) chứng minh BH×BD=BK×BC Cho mình xin cả hình nha