cho a= 1+3+3^2+3^3+...+3^2023, b=3^2023 tính b- 2a
TA
Những câu hỏi liên quan
a, cho a, b là 2 số thoả mãn |a-2b+3|^{2023} + (b-1)^{2024} 0. Tính giá trị biểu thứcP a^{2023} x b^{2024} + 2024b, 3 số hữu tỉ x,y,z thoả mãn xy+yz+zx 2023. Chứng tỏ rằng:A dfrac{left(x^2+2023right)xleft(y^2+2023right)xleft(z^2+2023right)}{16} viết được dưới dạng bình phương của 1 số hữu tỉ
Đọc tiếp
a, cho a, b là 2 số thoả mãn |a-2b+3|\(^{2023}\) + (b-1)\(^{2024}\) = 0. Tính giá trị biểu thức
P = a\(^{2023}\) x b\(^{2024}\) + 2024
b, 3 số hữu tỉ x,y,z thoả mãn xy+yz+zx = 2023. Chứng tỏ rằng:
A = \(\dfrac{\left(x^2+2023\right)x\left(y^2+2023\right)x\left(z^2+2023\right)}{16}\) viết được dưới dạng bình phương của 1 số hữu tỉ
a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)
\(\left(b-1\right)^{2024}>=0\forall b\)
Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)
Thay a=-1 và b=1 vào P, ta được:
\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)
Đúng 0
Bình luận (0)
Tính A-B Cho A= 1/2 +3/2^2 +3/2^3+...+3/2^2022
B= 2. 3/2^2023
A = \(\dfrac{1}{2}+\dfrac{3}{2}+\dfrac{3}{2^2}+\dfrac{3}{2^3}+.....+\dfrac{3}{2^{2021}}+\dfrac{3}{2^{2022}}\)
\(2\times\)A = 1 + 3+ \(\dfrac{3}{2}\) +\(\dfrac{3}{2^2}\) + \(\dfrac{3}{2^3}\)+...........+\(\dfrac{3}{2^{2021}}\)
2 \(\times\) A - A = 4 - \(\dfrac{1}{2}\) - \(\dfrac{3}{2^{2022}}\)
A = \(\dfrac{7}{2}\) - \(\dfrac{3}{2^{2022}}\)
B = 2 \(\times\dfrac{3}{2^{2023}}\)
A - B = \(\dfrac{7}{2}-\dfrac{3}{2^{2022}}\) - 2 \(\times\) \(\dfrac{3}{2^{2023}}\)
A - B = \(\dfrac{7}{2}\) - \(\dfrac{3}{2^{2022}}\) - \(\dfrac{3}{2^{2022}}\)
A - B = \(\dfrac{7}{2}\) - \(\dfrac{6}{2^{2022}}\)
A - B = \(\dfrac{7}{2}\) - \(\dfrac{3}{2^{2021}}\)
Đúng 2
Bình luận (0)
Tính A-B Cho A= 1/2 +(3/2)^2 +(3/2)^3+...+(3/2^)2022
B= 2. (3/2)^2023
Lời giải:
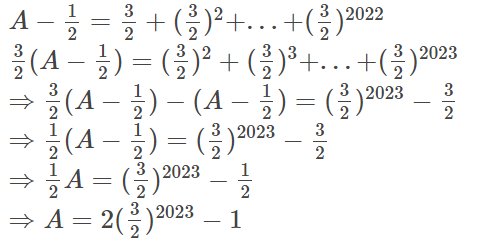
$\Rightarrow A-B=-1$
Đúng 0
Bình luận (0)
cho a+b+c khác 0 và a^3+b^3+c^3=2abc.a^(2023)+b^(2023)+c^(2023)/(a+b+c)^2023
Tính các tổng sau B = 1.3 + 2+3 mũ2 + 3 . 3 mũ 2 + ... + 2022 . 3 mũ 2022 + 2023 . 3 mũ 2023
Tính các tổng sau B = 1.3 + 2+3 mũ2 + 3 . 3 mũ 2 + ... + 2022 . 3 mũ 2022 + 2023 . 3 mũ 2023
Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
Đúng 0
Bình luận (0)
B = 1×3+2×3(mũ 2)+3×3(mũ 3)+...+2022×3(mũ 2022)+2023×3(mũ 2023)
\(3B=1.3^2+2.3^3+3.3^4+...+2022.3^{2023}+2023.3^{2024}\)
\(2B=3B-B=-3-3^2-3^3-...-3^{2023}+2023.3^{2024}\)
\(2B=2023.3^{2024}-\left(3+3^2+3^3+...+3^{2023}\right)\)
Đặt
\(C=3+3^2+3^3+...+3^{2023}\)
\(3C=3^2+3^3+3^4+...+3^{2024}\)
\(2C=3C-C=3^{2024}-3\Rightarrow C=\dfrac{3^{2024}-3}{2}\)
\(\Rightarrow2B=2023.3^{2024}-\dfrac{3^{2024}-3}{2}=\)
\(=\dfrac{2.2023.3^{2024}-3^{2024}+3}{2}=\dfrac{4045.3^{2024}+3}{2}\)
\(\Rightarrow B=\dfrac{4045.3^{2024}+3}{4}\)
Đúng 1
Bình luận (0)
cho a =1/3 - 2/3*2 + 3/3*3 - 4/3*4 + 5/3*5 - ...... + 2023/3*2023 - 2024/3*2024 hãy so sánh a với 20/3
Câu 1: Tính tổng
a, A = 1 + 3 + 3 mũ 2 + 3 mũ 3 +...+ 3 mũ 2012
b, B = 1 + 10 + 10 mũ 2 + 10 mũ 3 +...+ 10 mũ 2023
`#3107.101107`
1.
`a,`
\(A=1+3+3^2+3^3+...+3^{2012}\)
`3A = 3 + 3^2 + 3^3 + ... + 3^2013`
`3A - A = (3 + 3^2 + 3^3 + ... + 3^2013) - (1 + 3 + 3^2 + 3^3 + ... + 3^2012)`
`2A = 3 + 3^2 + 3^3 + ... + 3^2013 - 1 - 3 - 3^2 - 3^3 - ... - 3^2012`
`2A = 3^2013 - 1`
`=> A = (3^2013 - 1)/2`
Vậy, `A = (3^2013 - 1)/2`
`b,`
\(B=1+10+10^2+10^3+...+10^{2023}\)
`10B = 10 + 10^2 + 10^3 + ... + 10^2024`
`10 B - B = (10 + 10^2 + 10^3 + ... + 10^2024) - (1 - 10 + 10^2 + 10^3 + ... + 10^2023)`
`9B = 10 + 10^2 + 10^3 + ... + 10^2024 - 1 - 10^2 - 10^3 - ... - 10^2023`
`9B = 10^2024 - 1`
`=> B = (10^2024 - 1)/9`
Vậy, `B = (10^2024 - 1)/9.`
Đúng 3
Bình luận (0)
`a)A=1+3+3^2+3^3+...+3^2012`
`=>3A=3+3^2+3^3+...+3^2013`
`=>3A-A=2A=3^2013-1`
`=>A=(3^2013-1)/2`
`b)B=1+10+10^2+...+10^2024`
`=>10B=10+10^2+10^3+....+10^2025`
`=>10B-B=9B=10^2025-10`
`=>B=(10^2025-10)/9`
Đúng 0
Bình luận (3)