Trong mặt phẳng xOy, viết pt đường tròn C đường kính AB với A(-2,3) B(4,-5)
NN
Những câu hỏi liên quan
Câu 6: Trong mặt phẳng với hệ toạ độ Oxy a) Viết pt đường tròn (C) có đường kính AB biết A(-1;1) và B(0;2). b) Cho đường tròn (C): x^2 +y^2 -2x -4y+3=0.Viết pt tiếp tuyến của đường tròn (C) tại giao điểm của (C) với trục tung Oy
a, Đường tròn cần tìm có tâm \(I=\left(-\dfrac{1}{2};\dfrac{3}{2}\right)\), bán kính \(R=\dfrac{\sqrt{2}}{2}\)
Phương trình đường tròn: \(\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{1}{2}\)
b, (C) có tâm \(I=\left(1;2\right)\), bán kính \(R=\sqrt{2}\)
Giao điểm của (C) và trục tung có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x^2+y^2-2x-4y+3=0\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2-4y+3=0\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}y=1\\x=0\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm: \(M=\left(0;3\right);N=\left(0;1\right)\)
Phương trình tiếp tuyến tại M có dạng: \(\Delta_1:ax+by-3b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta_1\right)=\dfrac{\left|a+2b-3b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\)
\(\Leftrightarrow a^2+b^2-2ab=2a^2+2b^2\)
\(\Leftrightarrow\left(a+b\right)^2=0\)
\(\Leftrightarrow a=-b\)
\(\Rightarrow\Delta_1:x-y+3=0\)
Tương tự ta tìm được tiếp tuyến tại N: \(\Delta_2=x+y-1=0\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho điểm A(3,1) và đường thẳng (d): x+y-2=0
a) Viết pt đường tròn (C) tâm A tiếp xúc với đường thẳng (d)
b)Viết pt tiếp tuyến vs đường tròn (C) kẻ từ O(0,0)
c) Tính bán kính đường tròn (C') tâm A, biết (C') cắt (d) tại 2 điểm E,F sao cho diện tích tam giác AEF= 6
mong mọi người giúp e ạ
a.
\(R=d\left(A;d\right)=\dfrac{\left|3+1-2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Phương trình đường tròn:
\(\left(x-3\right)^2+\left(y-1\right)^2=2\)
b.
Tiếp tuyến d' qua O nên có dạng: \(ax+by=0\)
d' tiếp xúc (C) nên \(d\left(A;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\Leftrightarrow\left(3a+b\right)^2=2a^2+2b^2\)
\(\Leftrightarrow7a^2+6ab-b^2=0\Rightarrow\left(a+b\right)\left(7a-b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a+b=0\\7a-b=0\end{matrix}\right.\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;7\right)\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}x-y=0\\x+7y=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
Gọi M là trung điểm EF
\(\Rightarrow AM\perp EF\Rightarrow AM=d\left(A;d\right)=\sqrt{2}\)
\(S_{AEF}=\dfrac{1}{2}AM.EF=6\Rightarrow AM.EF=12\)
\(\Rightarrow EF=\dfrac{12}{\sqrt{2}}=6\sqrt{2}\)
\(\Rightarrow EM=\dfrac{EF}{2}=3\sqrt{2}\)
Áp dụng Pitago:
\(R'=AE=\sqrt{EM^2+AM^2}=2\sqrt{5}\)
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy A0;2), B(-2;-2), C(4;-2)
Viết phương trình đường tròn (C) có đường kính AB
\(\overrightarrow{BA}=\left(2;4\right)\Rightarrow AB=\sqrt{2^2+4^2}=2\sqrt{5}\)
Gọi M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}M\left(-1;0\right)\\AM=\dfrac{AB}{2}=\sqrt{5}\end{matrix}\right.\)
Đường tròn đường kính AB có tâm M và bán kính \(R=AM\) nên có pt:
\(\left(x+1\right)^2+y^2=5\)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ cho 2 điểm A(4;-1);B(-2;5). Viết phương trình đường tròn đường kính AB
Tọa độ tâm I là:
x=(4-2)/2=1 và y=(-1+5)/2=2
I(1;2); A(4;-1)
\(IA=\sqrt{\left(4-1\right)^2+\left(-1-2\right)^2}=3\sqrt{2}\)
=>Phương trình đường tròn là:
(x-1)^2+(y-2)^2=18
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(1;2), B(3;-1), C(-2;1)
a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
b) Viết phương trình đường tròn đường kính AB
a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
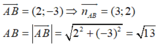
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
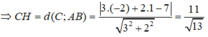
Diện tích tam giác ABC là:
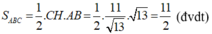
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
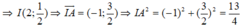
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
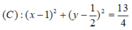
Đúng 0
Bình luận (0)
Câu 12: Trong mặt phẳng tọa độ, cho A(-1;-3),B(-3;5). a. Viết phương trình tham số của đường thẳng AB. b. Viết phương trình đường tròn đường kính AB.
\(AB\left\{{}\begin{matrix}quaA\left(-1;-3\right)\\VTCP\overrightarrow{AB}=\left(-2;8\right)\end{matrix}\right.\)
\(PTTS\) của \(AB:\left\{{}\begin{matrix}x=-1-2t\\y=-3+8t\end{matrix}\right.\)
Gọi \(I\left(x_I;y_I\right)\) là tâm đường tròn
\(I\) là trung điểm \(AB\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-3+5}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(-2;1\right)\)
\(AB=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Mà \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{17}}{2}=\sqrt{17}\)
Vậy \(PT\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=17\)
Đúng 3
Bình luận (1)
Câu 3: Trong mặt phẳng Oxy, cho hai điểm A(1;-2), B(3;1). Viết phương trình tham số của đường thẳng d đi qua hai điểm A và B.
Câu 4: Cho hai điểm A(4; -3), B(2;1). Viết phương trình đường tròn (C) nhận AB làm đường kính
Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-30. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó. A.
21
. B.
2
6
. C. 6. D.
3
3
.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-3=0. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A. 21 .
B. 2 6 .
C. 6.
D. 3 3 .
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 0 a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng 4sqrt{5}.Tìm tọa độ các giao điểm của d và (C)b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng 5sqrt{3}
Đọc tiếp
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 = 0
a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng \(4\sqrt{5}\).Tìm tọa độ các giao điểm của d và (C)
b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng \(5\sqrt{3}\)
a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)