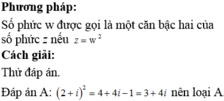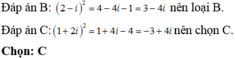ìm các căn bậc hai của số phức sau: -i; 4i; -4;1+4 √3 i
LD
Những câu hỏi liên quan
Cho các mệnh đề sau(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm(II) Trên tập hợp các số phức thì số thực âm không có căn bậc hai(III) Môđun của một số phức không phải là một số phức(IV) Môđun của một số phức là một số thực dươngTrong bốn mệnh đề trên có bao nhiêu mệnh đề đúng? A. 2 B. 4 C. 3 D. 1
Đọc tiếp
Cho các mệnh đề sau
(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm
(II) Trên tập hợp các số phức thì số thực âm không có căn bậc hai
(III) Môđun của một số phức không phải là một số phức
(IV) Môđun của một số phức là một số thực dương
Trong bốn mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 2
B. 4
C. 3
D. 1
Đáp án D
(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm.
Đúng 0
Bình luận (0)
Tìm các căn bậc hai phức của các số sau:
-7;-8;-12;-20;-121
Tìm các căn bậc hai phức của các số sau : \(-7;-8;-12;-20;-121\) ?
± i√7 ; ± i2√2 ; ± i2√3; ± i2√5 ; ± 11i
Đúng 0
Bình luận (0)
Số nào sau đây là một căn bậc hai của số phức 3 +4i?
A. 1 -2i
B. 1 +2i
C. 2 +i
D. 2 -i
Số phức nào dưới đây là một căn bậc hai của số phức
z
-
3
+
4
i
? A.
2
+
i
B.
2
-
i
C.
1
+
2
i
D.
1
-
2
i
Đọc tiếp
Số phức nào dưới đây là một căn bậc hai của số phức z = - 3 + 4 i ?
A. 2 + i
B. 2 - i
C. 1 + 2 i
D. 1 - 2 i
Số phức nào dưới đây là một căn bậc hai của số phức z=-3+4i?
![]()
![]()
![]()
![]()
a) Đọc các số sau: \(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82} \)
b) Viết các số sau: căn bậc hai số học của 39; căn bậc hai số học của \(\frac{9}{{11}}\); căn bậc hai số học của \(\frac{{89}}{{27}}\)
a) \(\sqrt {15} \) đọc là: căn bậc hai số học của mười lăm
\(\sqrt {27,6} \) đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu
\(\sqrt {0,82} \) đọc là: căn bậc hai số học của không phẩy tám mươi hai
b) Căn bậc hai số học của 39 viết là: \(\sqrt {39} \)
Căn bậc hai số học của \(\frac{9}{{11}}\) viết là: \(\sqrt {\frac{9}{{11}}} \)
Căn bậc hai số học của \(\frac{{89}}{{27}}\) viết là: \(\sqrt {\frac{{89}}{{27}}} \)
Đúng 0
Bình luận (0)
Căn bậc hai của số phức z-25 là
x
1
,
2
±
5
không tồn tại
x
1
,
2
±
25
i
x
1
,
2...
Đọc tiếp
Căn bậc hai của số phức z=-25 là
x 1 , 2 = ± 5
không tồn tại
x 1 , 2 = ± 25 i
x 1 , 2 = ± 5 i
Căn bậc hai của số phức z = − 25 là
A. x 1,2 = ± 5
B. Không tồn tại
C. x 1,2 = ± 25 i
D. x 1,2 = ± 5 i
Đáp án D.
Cách 1: Tư duy tự luận
z = − 25 = 25. − 1 = 25 i 2 → z 1,2 = ± 5 i
Cách 2: Sử dụng máy tính cầm tay

Vậy các căn bậc hai của số phức z là z 1,2 = ± 5 i
Đúng 0
Bình luận (0)