Giúp mình câu c ạ!

giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Giúp mình câu c với ạ, chỉ cần câu c thôi ạ!

Vì \(\widehat{MIA}=90^0\left(\text{góc nt chắn nửa đường tròn}\right)\) nên \(MI\perp IA\)
Xét \(\Delta MBP\) có \(\left\{{}\begin{matrix}PK\perp MB\left(PK\perp MN\right)\\MI\perp PB\left(MI\perp IA\right)\\\left\{H\right\}=PK\cap MI\end{matrix}\right.\) nên H là trực tâm
Do đó \(HB\perp PM\)
Mà \(AM\perp PM\Rightarrow HB\text{//}AM\)
Vì \(HB\text{//}OA\Rightarrow\dfrac{PB}{PA}=\dfrac{HB}{OA}\)
Ta có \(\sin MPB=\sin MPA=\dfrac{MA}{PA}=\dfrac{2OA}{PA}\)
\(\Rightarrow\dfrac{1}{2}BP\cdot\sin MPB=\dfrac{PB\cdot\dfrac{2OA}{PA}}{2}=\dfrac{PB\cdot2OA}{2PA}=\dfrac{PB}{PA}\cdot OA=\dfrac{HB}{OA}\cdot OA=HB\left(đpcm\right)\)
GIÚP mình câu C vs ạ :((( mình cần câu C nhấtt
Giúp mình câu c vs ạ mình cần gấp ạ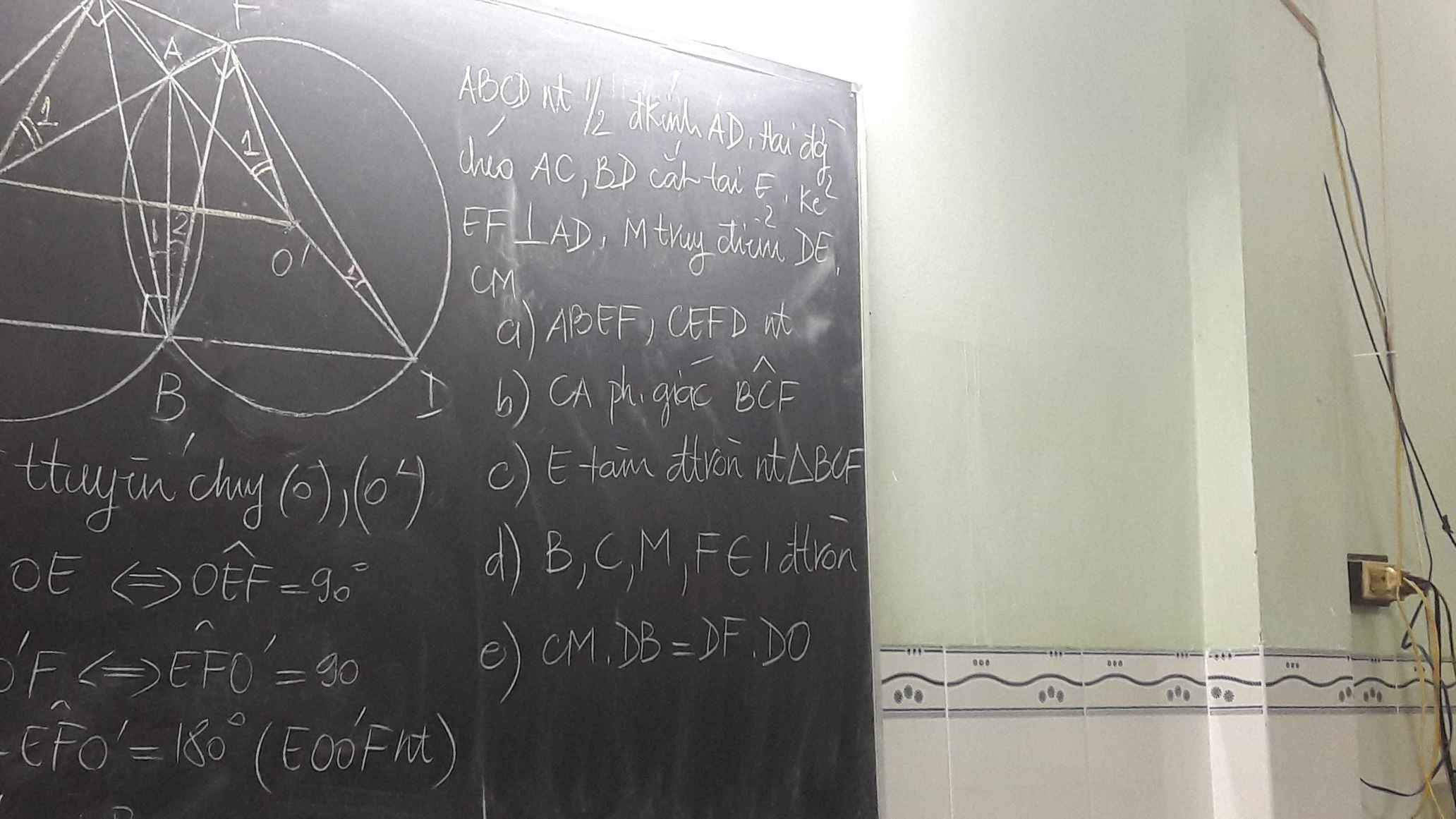
Các bạn giúp mình câu b;c;d;e ạ. Các bạn làm được câu nào thì làm ạ, còn bạn nào giỏi giúp mình nhiều hơn thì tốt ạ! 
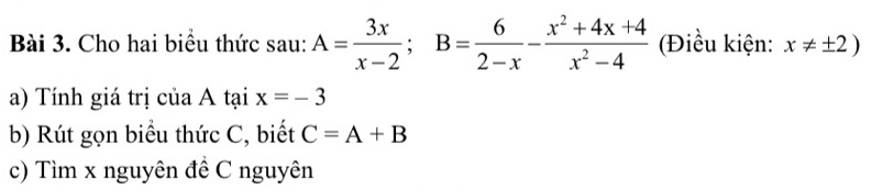
Giúp mình câu b và c với ạ, mình cảm ơn rất nhiều ạ
a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)
 giúp mình câu c với ạ, 2 câu trên mình biết làm rồi
giúp mình câu c với ạ, 2 câu trên mình biết làm rồi
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\)
a. PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PTHH: \(n_{Fe}=n_{H_2}=1,5\left(mol\right)\)
\(\Rightarrow m_{Fe}=56\cdot1,5=84\left(g\right)\)
b. Đổi: \(500ml=0,5l\)
\(CM_{H_2SO_4}=\dfrac{1,5}{0,5}=3M\)
c. \(2H_2+O_2\rightarrow2H_2O\)
Theo PTHH: \(n_{O_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot1,5=0,75\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,75\cdot22,4=16,8\left(l\right)\)
c, \(2H_2+O_2 \rightarrow2H_2O\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5(mol) \Rightarrow n_{O_2}=0,75(mol)\)
\(V_{O_2}=22,4.0,75=16,8(l)\)
a) Fe+H2SO4---->FeSO4+H2(1)
nH2=33,6:22,4=1,5 mol
Theo PT(1):nFe=nH2=1,5 mol
=>mFe=56.1,5=84g
b)TheoPT(1):nH2SO4=nH2=1,5 mol
=>CM(H2SO4)=1,5:0,5=3 M
c)2H2+O2---->2H2O(2)
TheoPT(2):nO2=1/2nH2=1/2.1,5=0,75mol
=>VO2=22,4.0,75=16,8l
Giúp mình câu b và câu c ạ 
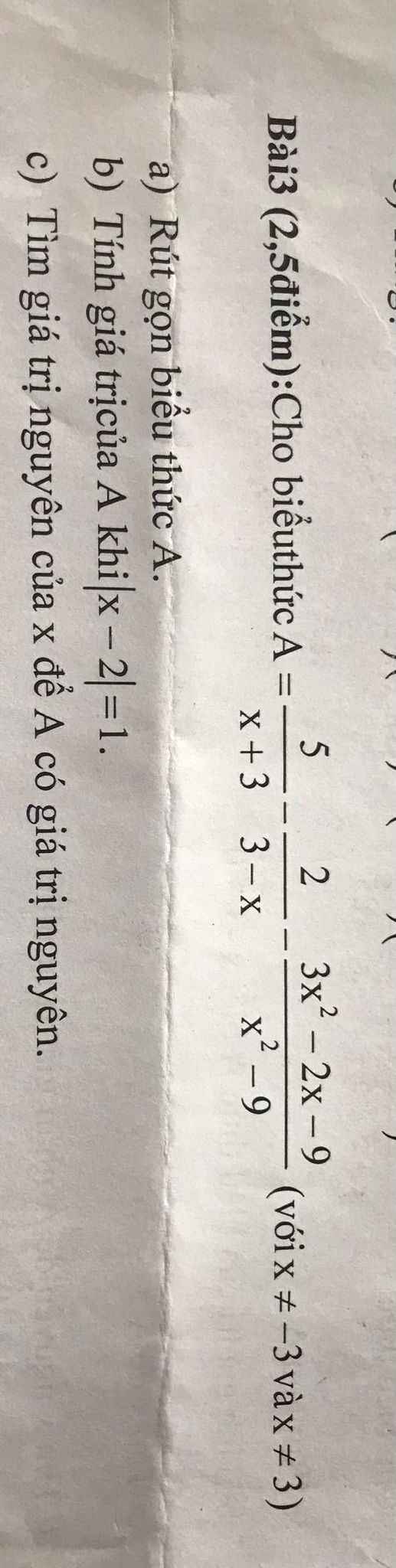
Giúp mình câu c với ạ, mình cần gấp
\(a,A=\dfrac{5x-15+2x+6-3x^2+2x+9}{\left(x-3\right)\left(x+3\right)}=\dfrac{-3x^2+9x}{\left(x-3\right)\left(x+3\right)}\\ A=\dfrac{-3x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{-3x}{x+3}\\ b,\left|x-2\right|=1\Leftrightarrow\left[{}\begin{matrix}x-2=1\\2-x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\\ \Leftrightarrow A=\dfrac{-3\cdot1}{1+3}=\dfrac{-3}{4}\\ c,A=\dfrac{-3\left(x+3\right)+9}{x+3}=-3+\dfrac{9}{x+3}\in Z\\ \Leftrightarrow x+3\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\\ \Leftrightarrow x\in\left\{-12;-6;-4;-2;0;6\right\}\left(tm\right)\)
Giúp mình câu c vs ạ mình cảm ơn.
a) Xét \(\left(O\right):\)
+) Ta có: Dây AB = Dây AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}.\)
+) \(\widehat{ABM}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
Mà \(\stackrel\frown{AB}=\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\widehat{ABM}=\widehat{ABC}.\)
\(\Rightarrow\) BA là phân giác \(\widehat{CBM}.\)
b) Xét \(\left(O\right):\)
\(\widehat{MBA}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{MDB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc nội tiếp).
\(\Rightarrow\widehat{MBA}=\widehat{MDB}.\)
Xét \(\Delta MAB\) và \(\Delta MBD:\)
\(\widehat{MBA}=\widehat{MDB}.\)
\(\widehat{BMD}chung.\)
\(\Rightarrow\Delta MAB\sim\Delta MBD\left(g-g\right).\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{MB}{MD}\) (Cặp cạnh tương ứng tỉ lệ).
\(\Rightarrow MA.MD=MB^2.\)