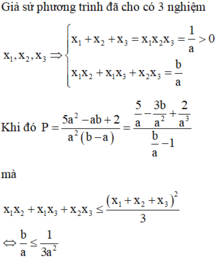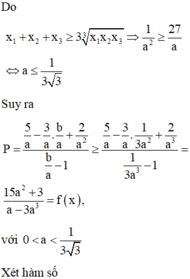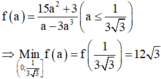Tìm a,b sao cho x4+ax3+bx-1 chia hết cho x2-1
NA
Những câu hỏi liên quan
Tìm a,b để đa thức : x4+ax3+bx-1 chia hết cho x2-1
MN làm giúp mình nha càng nhanh thì càng xing gái đẹp trai :3333
\(x^4+ax^3+bx-1=\left(x^2-1\right)\left(x^2+1\right)+ax\left(x^2-1\right)+\left(a+b\right)x\)
\(\Rightarrow x^4+ax^3+bx-1\) chia hết cho \(x^2-1\) khi \(a+b=0\)
\(\Leftrightarrow b=-a\)
(Chỉ cần a; b là 2 số đối nhau là đủ, có vô số cặp a;b thỏa mãn đề bài, ví dụ (a;b)=(1;-1); (2;-2); (3;-3)... đều đúng)
Đúng 1
Bình luận (1)
tìm a và b để
a) x4-9x3+21x2+ax+b chia hết cho x2-x-2
b) x4-7x3+10x2+(a-1)x+b-a chia hết cho x2-6x+5
tìm a,b sao cho f(x)= ax3 +bx2 +10x - 4 chia hết cho đa thức g(x) = x2 +x - 2
Tìm a sao cho biểu thức A chia hết cho B(tìm a sao cho A:B ∈ Z)
1)A=x3-3x2-ax+3;B=x-1
2)A=3x3-16x2+25x+a;B=x2-4x+3
3)A=x4-x3+6x2-x+a;B=x2-x+5
\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
Đúng 4
Bình luận (0)
Xét phương trình
a
x
3
−
x
2
+
b
x
−
1
0
với a, b là các số thực,
a
≠
0
,
a
≠
b
sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2...
Đọc tiếp
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Xét phương trình ax3- x2+ bx-10 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2
-
3
a
b
+
2
a
2
(
b
-...
Đọc tiếp
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
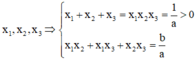
Khi đó
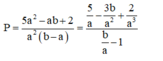
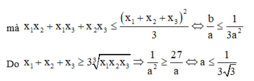
Suy ra
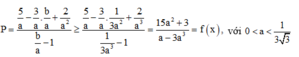
Xét hàm số:
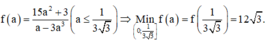
Chọn D.
Đúng 0
Bình luận (0)
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]f(x)ax4+bx3+cx2+dx+ef(x)ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.Cm đa thức không có nghiệm hữu tỉ2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZCmR các hệ số của P(x) chia hết cho 7.3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)10; P(2)20; P(3)30.Tính P(12)+P(−8)10P(12)+P(−8)104. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)5. Tìm đa thức bậc 3 có hệ số cao...
Đọc tiếp
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))
123456
tìm a b c sao cho đa thức x4 + ax2 + bx + c chia hết cho đa thuc ( x - 3 )3
(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a/ Tìm a sao cho đa thức : x4 – x3 + 6x2 – x + a chia hết cho đa thức: x2 – x + 5
b/ Tính giá trị nguyên của n để giá trị của biểu thức : 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức: 3n + 1
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
Đúng 1
Bình luận (0)
Tìm hai số thực a và b để đa thức ax3 +x2-x+b chia hết cho đa thức x2+3x+2.
- Để hai đa thức trên chia cho nhau hết thì :\(\left\{{}\begin{matrix}7a-4=0\\b-2\left(1-3a\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7a=4\\6a+b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{4}{7}\\b=-\dfrac{10}{7}\end{matrix}\right.\)
Vậy ...
Đúng 2
Bình luận (1)