1.

Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)

\(f\left(x\right)\) xác định và liên tục trên R

\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)

\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)

\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)

\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)

\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)

\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)

\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)

\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)

Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt

2.

Đặt \(t=g\left(x\right)=x.cosx\)

\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)

\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)

Hàm \(f\left(t\right)\) xác định và liên tục trên R

\(f\left(1\right)=1>0\)

\(f\left(-2\right)=-8< 0\)

\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m

3. Chắc ngoặc thứ là \(\left(2m^2-2m+4040\right)\) ?

\(\Leftrightarrow\left(m^2-m+2021\right)x^3-2\left(m^2-m+2020\right)x^2-4x+m^2-m+2021=0\)

Do \(m^2-m+2020>0\), đặt \(m^2-m+2020=n^2\)

\(\Rightarrow\left(n^2+1\right)x^3-2n^2x^2-4x+n^2+1=0\)

Quy về bài số 1

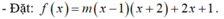
- Tập xác định của hàm số f(x) là D = R.

- Vì f(x) là hàm đa thức nên f(x) liên tục trên R.

- Ta có:

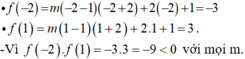
- Do đó,phương trình f(x) = 0 luôn có ít nhất 1 nghiệm trong khoảng (- 2; 1) với mọi m.

→ Kết luận phương trình (1) luôn có nghiệm với mọi giá trị m.

Đặt \(f\left(x\right)=\left(m^2-m+1\right)x^4-3x^3-1\)

\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng trên R

\(f\left(0\right)=-1< 0\)

\(f\left(3\right)=81\left(m^2-m+1\right)-55=81\left(m-\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\)

\(\Rightarrow f\left(0\right).f\left(3\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(0;3\right)\)

\(f\left(-1\right)=m^2-m+2=\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)

\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)

\(\Rightarrow\) Pt có ít nhất 2 nghiệm thuộc \(\left(-1;3\right)\Rightarrow\) có ít nhất 2 nghiệm trên \(\left(-5;5\right)\)

Lời giải:

Dễ thấy 2 PT trên đều có 2 nghiệm phân biệt.

Đối với PT $(1)$, nếu $x_1,x_2$ là 2 nghiệm của  nó, áp dụng định lý Viet ta có:

\(\left\{\begin{matrix} x_1+x_2=3\\ x_1x_2=-m^2\end{matrix}\right.\)

\(\Rightarrow \frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1x_2}=-\frac{3}{m^2}\); \(\frac{1}{x_1}.\frac{1}{x_2}=\frac{-1}{m^2}\)

Theo định lý Viet đảo, $\frac{1}{x_1}, \frac{1}{x_2}$ là nghiệm của PT:

\(x^2+\frac{3}{m^2}x-\frac{1}{m^2}=0\Leftrightarrow m^2x^2+3x-1=0\)

Do đó ta có đpcm.

Đặt \(f\left(x\right)=\left(m^2-5m+11\right)x^{2021}+2x^2+1\)

\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng thuộc R

\(f\left(0\right)=1>0\)

\(f\left(-1\right)=-\left(m^2-5m+11\right)+3=-\left(m-\dfrac{5}{2}\right)^2-\dfrac{7}{4}< 0\) ; \(\forall m\)

\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\) ; \(\forall m\)

\(\Rightarrow\) Pt đã cho luôn có ít nhất 1 nghiệm thuộc (-1;0) với mọi m

Có : \(m^2+m+1>0\) với mọi m 

=> \(\left(m^2+m+1\right)x^4+2x-2=0\)là phương trình bậc  4 với mọi m

Đặt: \(f\left(x\right)=\left(m^2+m+1\right)x^4+2x-2\)

Ta có: \(f\left(0\right)=-2< 0\)với mọi m 

\(f\left(1\right)=m^2+m+1>0\) với mọi m 

=> Tồn tại \(a\in\left(0;1\right)\) sao cho \(f\left(a\right)=0\) với mọi m 

=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2=0\) có nghiệm thuộc ( 0; 1) với mọi m 

=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2\)=0 có nghiệm với mọi m.

Ở dòng thứ 6 bạn thêm 1 chút để chặt chẽ hơn:

Vì f(0). f(1) < 0 => tồn tại....

Lời giải:

Để pt có 2 nghiệm $x_1,x_2$ thì:

$\Delta'=1+(3+m)=4+m\geq 0\Leftrightarrow m\geq -4$ (chứ không phải với mọi m như đề bạn nhé)!

Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-2\\ x_1x_2=-(m+3)\end{matrix}\right.\)

$x_1, x_2\neq 0\Leftrightarrow -(m+3)\neq 0\Leftrightarrow m\neq -3$

$\frac{x_1}{x_2}-\frac{x_2}{x_1}=\frac{-8}{3}$

$\Leftrightarrow \frac{x_1^2-x_2^2}{x_1x_2}=\frac{-8}{3}$

$\Leftrightarrow \frac{-2(x_1-x_2)}{-(m+3)}=\frac{-8}{3}$
$\Leftrightarrow x_1-x_2=\frac{4}{3}(m+3)$

$\Rightarrow (x_1-x_2)^2=\frac{16}{9}(m+3)^2$

$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=\frac{16}{9}(m+3)^2$
$\Leftrightarrow 4+4(m+3)=\frac{16}{9}(m+3)^2$

$\Leftrightarrow m+3=3$ hoặc $m+3=\frac{-3}{4}$

$\Leftrightarrow m=0$ hoặc $m=\frac{-15}{4}$ (đều thỏa mãn)

a:Δ=(2m-2)^2-4(-m-3)

=4m^2-8m+4+4m+12

=4m^2-4m+16

=(2m-1)^2+15>=15>0

=>Phương trình luôn có hai nghiệm phân biệt

b: Để phương trình có hai nghiệm trái dấu thì -m-3<0

=>m+3>0

=>m>-3

c: Để phương trình có hai nghiệm âm thì:

2m-2<0 và -m-3>0

=>m<1 và m<-3

=>m<-3

d: x1^2+x2^2=(x1+x2)^2-2x1x2

=(2m-2)^2-2(-m-3)

=4m^2-8m+4+2m+6

=4m^2-6m+10

=4(m^2-3/2m+5/2)

=4(m^2-2*m*3/4+9/16+31/16)

=4(m-3/4)^2+31/4>0 với mọi m