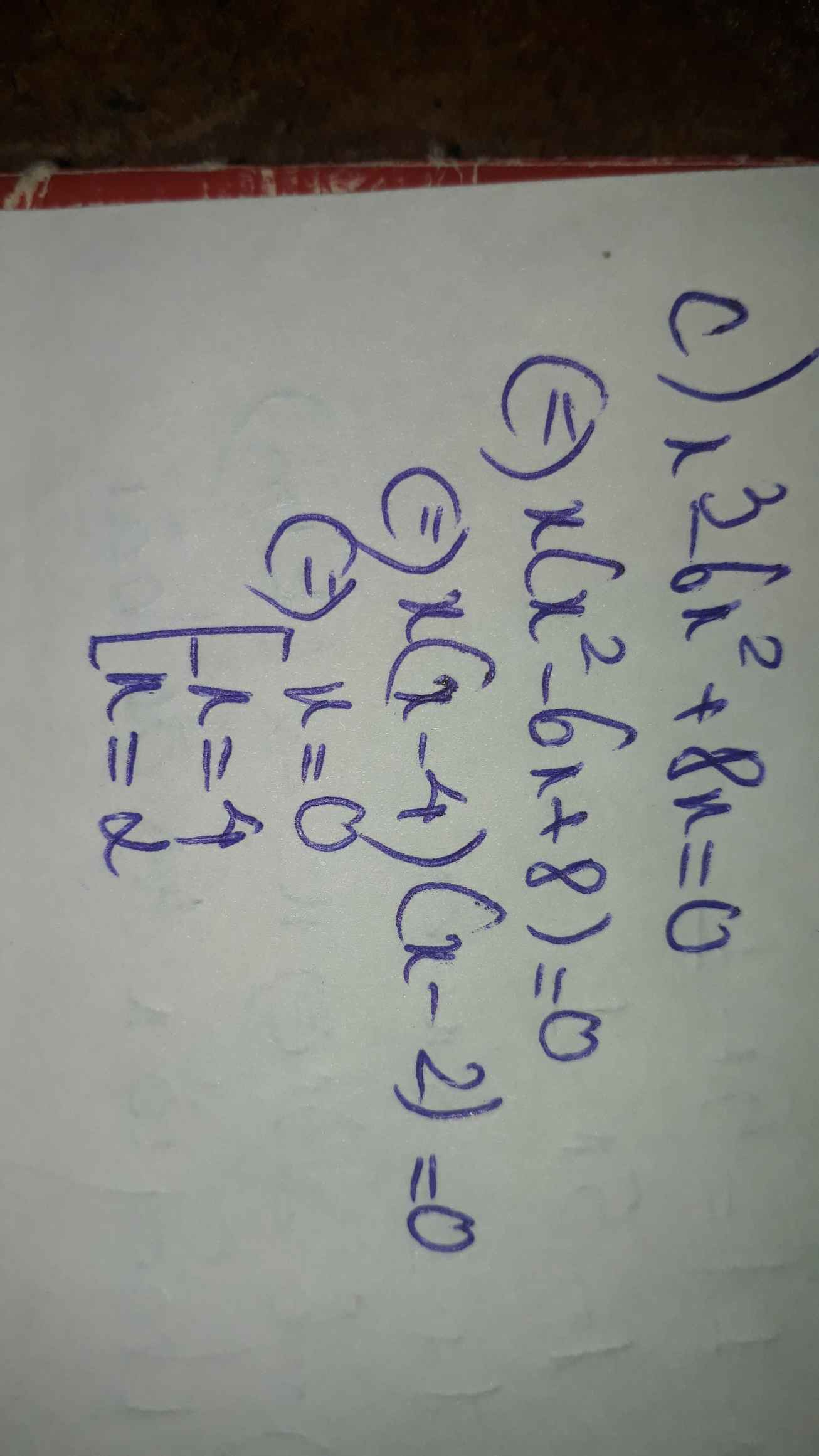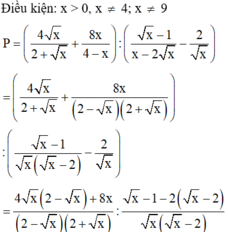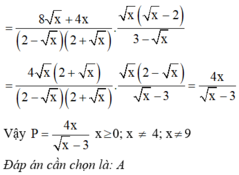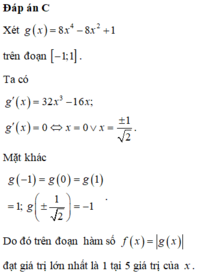Tìm x, biết: 8x4+x=0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HY
Những câu hỏi liên quan
Tìm x:
a) (x-3)(x2+3x+9)-x(x2-3)=0
b) 8x4+x=0
d) x3-6x2+8x=0
a: Ta có: \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x^2-3\right)=0\)
\(\Leftrightarrow x^3-27-x^3+3x=0\)
\(\Leftrightarrow x=9\)
b: Ta có: \(8x^4+x=0\)
\(\Leftrightarrow x\left(8x^3+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)\left(4x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho biểu thức
P
4
x
2
+
x
+
8
x
4
-
x
:
x
-...
Đọc tiếp
Cho biểu thức P = 4 x 2 + x + 8 x 4 - x : x - 1 x - 2 x - 2 x với x ≥ 0;x ≠ 4; x ≠ 9.
A. P = 4 x x - 3
B. P = 4 x x + 3
C. P = x x - 3
D. P = - 4 x x - 3
Tìm x:
a.(x-1)^x+2=(x-1)^x+4
b.1/4x2/6x3/8x4/10x5/12x...x30/62x31/42=2x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của
y
8
x
4
-
8
x
2
+
1
với
x
∈
1
2
;
1
.
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của y = 8 x 4 - 8 x 2 + 1 với x ∈ 1 2 ; 1 .
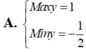
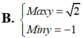
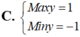
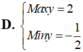
Tìm giá trị biểu thức :
\(\frac{6^{10}x-3^7}{9^8x4^5}\)
Cho hàm số
f
(
x
)
|
8
x
4
+
a
x
2
+
b
|
, trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn...
Đọc tiếp
Cho hàm số f ( x ) = | 8 x 4 + a x 2 + b | , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn khẳng định đúng?
A. 
, 
B. 
, 
C. 
, 
D. 
, 
Đáp án C
Đặt 
khi đó ta có 
.
Vì 
nên 
.
Theo yêu cầu bài toán thì ta có: 
với mọi 
và có dấu bằng xảy ra.
Đồ thị hàm số 
là một parabol có bề lõm quay lên trên do đó điều kiện trên dẫn đến hệ điều kiện sau xảy ra :
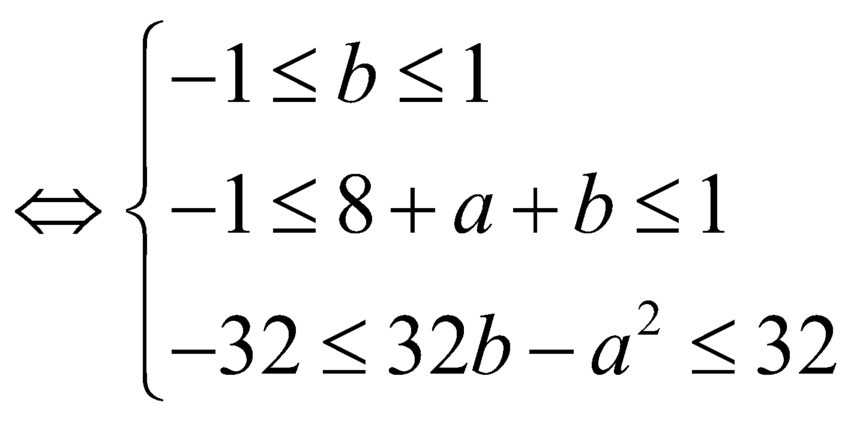
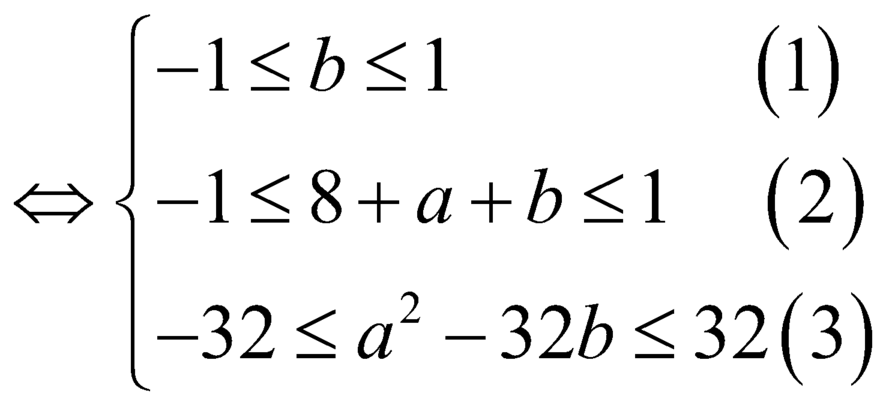
Lấy 
ta có : 
do đó 
.
Lấy 
ta có : 
Suy ra : 
.
Khi đó ta có 
và 
.
Kiểm tra : 
Vì 
nên 
.
Vậy 
khi 
(t/m).
Đúng 0
Bình luận (0)
Cho hai đa thức:
P
x
-
5
x
3
-
1
3
+
8
x
4
+
x
2
và
Q
x
2
-
5
x
-
3
x
3
+
x...
Đọc tiếp
Cho hai đa thức:
P
x
=
-
5
x
3
-
1
3
+
8
x
4
+
x
2
và Q = x 2 - 5 x - 3 x 3 + x 4 - 2 3
Hãy tính P(x) + Q(x) và P(x) – Q(x).
Sắp xếp hai đa thức theo lũy thừa giảm dần của biến rồi sau đó thực hiện phép tính:
Đúng 0
Bình luận (0)
Hàm số f ( x ) = 8 x 4 - 8 x 2 + 1 đạt giá trị lớn nhất trên đoạn [-1;1] tại bao nhiêu giá trị của x ?
A. 3
B. 2
C. 5
D. 4
Tính giá trị các đa thức sau tại GTTĐ của x=1
a) f(x)= x2+2x2+3x3+...+2018x2018+2019x2019
b) g(x) = 2x+4x2+6x3+8x4+...+200x100202x101