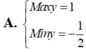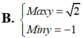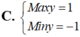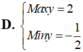Các câu hỏi tương tự
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây đúng?
A. m > 10
B. 8 < m < 10
C. 0 < m < 4
D. 4 < m < 8
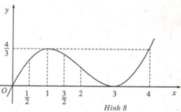
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
x
-
2
+
4
-
x
lần lượt là M và m. Chọn câu trả lời đúng. A. M 4, m 2 B. M 2, m 0 C. M 3, m 2 D. M 2, m
2
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x lần lượt là M và m. Chọn câu trả lời đúng.
A. M = 4, m = 2
B. M = 2, m = 0
C. M = 3, m = 2
D. M = 2, m = 2
Trong không gian với hệ trục Oxyz, cho mặt cầu
(
S
)
:
(
x
+
1
)
2
+
(
y
-
4
)
2
+
z
2
8
và điểm A(3;0;0); B(4;2;1). Điểm M thay...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y - 4 ) 2 + z 2 = 8 và điểm A(3;0;0); B(4;2;1). Điểm M thay đổi nằm trên mặt cầu, tìm giá trị nhỏ nhất của biểu thức P=MA+2MB.
A. P= 2 2
B. 3 2
C. 4 2
D. 6 2
Cho số phức zx+yi với x, y là các số thực không âm thỏa mãn
z
-
3
z
-
1
+
2
i
1
và biểu thức
P
z
2
-...
Đọc tiếp
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i = 1 và biểu thức P = z 2 - z - 2 + i ( z 2 - z - 2 ) z ( 1 - i ) + z ¯ ( 1 + i ) . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].
Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 = 2i|.
A. 8 và 4
![]()
![]()
![]()
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x 4 – 4 x 2 + 1 trên đoạn [-1; 2]
Cho hàm số y
-
x
2
+
2
n
ế
u
-
2
≤
x
≤...
Đọc tiếp
Cho hàm số y =
-
x
2
+
2
n
ế
u
-
2
≤
x
≤
1
x
n
ế
u
1
<
x
≤
3
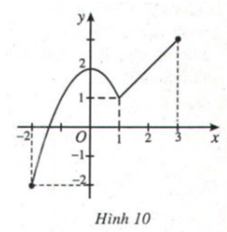
Có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.