 Giups mình câu b ạ
Giups mình câu b ạ
TH
Những câu hỏi liên quan
Giups mình câu này với ạ, mình cmon:(
giups mình câu i và câu L đến hết, cảm ơn ạ
i: ĐKXĐ: \(\left[{}\begin{matrix}x\ge\sqrt{5}+1\\x\le-\sqrt{5}+1\end{matrix}\right.\)
l:ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-5\end{matrix}\right.\)
m: ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x\le3\end{matrix}\right.\)
n: ĐKXĐ: \(x\in R\)
Đúng 1
Bình luận (0)
Giups mình câu này với ạ mình đang cần gấp để ôn thi mình cảm ơn trước
Giups mình câu này với ạ mình đang cần gấp để ôn thi mình cảm ơn trước
1 eats => has eaten
2 buy => bought
3 took => take
4 ate => eat
5 and => so
6 so => as
7 photo => photography
8 are, either => were, too
9 the puppets => puppets
10 take => takes
Đúng 1
Bình luận (0)
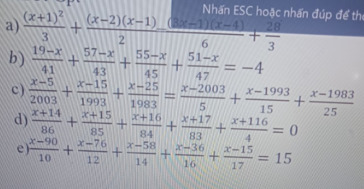
Giups mik câu a-b-d với ạ
d: \(\Leftrightarrow\dfrac{x+14}{86}+1+\dfrac{x+15}{85}+1+\dfrac{x+16}{84}+1+\dfrac{x+17}{83}+1+\dfrac{x+116}{4}-4=0\)
=>x+100=0
hay x=-100
a: \(\Leftrightarrow2\left(x+1\right)^2+3\left(x^2-3x+2\right)=\left(3x-1\right)\left(x-4\right)+56\)
\(\Leftrightarrow2x^2+4x+2+3x^2-9x+6-\left(3x^2-13x+4\right)-56=0\)
\(\Leftrightarrow5x^2-5x-48-3x^2+13x-4=0\)
\(\Leftrightarrow2x^2+8x-52=0\)
\(\Leftrightarrow x^2+4x-13=0\)
\(\Leftrightarrow\left(x+2\right)^2=17\)
hay \(x\in\left\{-\sqrt{17}-2;\sqrt{17}-2\right\}\)
Đúng 1
Bình luận (0)
em mình hỏi một câu :
Em hãy tìm từ có âm là D và còn vần là au .
Giups với ạ, khó quá mình chẳng nghĩ ra ...
giups mình câu này với ạ, ghi rõ cách làm và đáp án ra ạ, cảm ơn các bạn!
ai giups em câu b với ạ em cảm ơn nhiều!!
Pt hoành độ giao điểm:
\(x^2=-2\left(m-2\right)x-m^2+4m\Leftrightarrow x^2+2\left(m-2\right)x+m^2-4m=0\) (1)
\(\Delta'=\left(m-2\right)^2-\left(m^2-4m\right)=4>0;\forall m\Rightarrow\) (1) luôn có 2 nghiệm pb hay (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m-2\right)\\x_1x_2=m^2-4m\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow\left[{}\begin{matrix}m\ne0\\m\ne4\end{matrix}\right.\)
Khi đó:
\(\dfrac{3}{x_1}+x_2=\dfrac{3}{x_2}+x_1\Leftrightarrow\left(3+x_1x_2\right)x_2=\left(3+x_1x_2\right)x_1\)
\(\Leftrightarrow\left(3+x_1x_2\right)\left(x_1-x_2\right)=0\)
\(\Leftrightarrow3+x_1x_2=0\) (do \(\Delta>0\) nên \(x_1-x_2\ne0\) với mọi m)
\(\Leftrightarrow3+m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=1\\m=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giups mình bài 9 với ạ!
Mình cần ngay ạ


