cho tam giác DEF có 2 đường trung tuyến EM,FN cắt nhau tại G biết góc MEF>góc NFE so sánh EM và FN
46
Những câu hỏi liên quan
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.
Cho tam giác DEF cân tại D (góc D<90 độ ).kẻ EM vuông góc với AC (M thuộc AC ),kẻ FN vuông góc với AB ( N thuộc AB) ,EM và FNcat81 nhau tại H.Chứng minh rằng :
a) tam giác EMF =tam giác FNE
b) DH là đường trung trực của EF
a)xét ΔEMF và ΔFNE có:
\(\widehat{EMF}\)=\(\widehat{FNE}\)=\(90^o\)
EF là cạnh chung
\(\widehat{MFE}\)=\(\widehat{NEF}\)(ΔDEF cân tại D)
\(\Rightarrow\)ΔEMF=ΔFNE(cạnh huyền góc nhọn)
vì ΔDEF cân tại D \(\Rightarrow\)DE=DF
mà EN=FM
\(\Rightarrow\)DE-EN=DF-FM
hay DN=DM
b)xét ΔDHN và ΔDHM có:
\(\widehat{DNH}\)=\(\widehat{DMH}\)=\(90^o\)
DN=DM(ch/m trên)
DH là cạnh chung
\(\Rightarrow\)ΔDHN=ΔDHM(cạnh huyền cạnh góc vuông)
\(\Rightarrow\)\(\widehat{MDH}\)=\(\widehat{NDH}\)(2 góc tương ứng)
kéo dài DH cắt EF tại O ta được:
xét ΔDOF và ΔDOE có:
DE=DF(ΔDEF cân tại D)
\(\widehat{FDO}\)=\(\widehat{EDO}\)(ch/m trên)
\(\widehat{DEO}\)=\(\widehat{DFO}\)(ΔDEF cân tại D)
\(\Rightarrow\)ΔDOF=ΔDOE(g-c-g)
\(\Rightarrow\widehat{DOE}=\widehat{DOF}\)(2 góc tương ứng)(1)
OE=OF(2 cạnh tương ứng)(2)
Mà \(\widehat{DOE}+\widehat{DOF}=180^o\)(2 góc kề bù)(3)
Từ (1)và(3)\(\Rightarrow\)\(\widehat{DOE}=\widehat{DOF}=\dfrac{180^o}{2}=90^o\)(4)
Từ (2)và(4)\(\Rightarrow\)DH là trung trực của EF(đ.p.cm)
Đúng 1
Bình luận (0)
Cho tam giác nhọn DEF , đường cao EM , FN cắt nhau tại I
a) CM tam giác DME \(\sim\)DNF
b)IM.IE =IN.IF
c)Cho góc EDF =45 độ . Chứng tỏ rằng :\((\dfrac{MN}{EF})^2\) =\(\dfrac{1}{2}\)
a: Xet ΔDME vuông tại M và ΔDNF vuông tại N có
góc D chung
=>ΔDME đồng dạng với ΔDNF
b: Xet ΔINE vuông tại N và ΔIMF vuông tại M có
góc NIE=góc MIF
=>ΔINE đồng dạng với ΔIMF
=>IN/IM=IE/IF
=>IN*IF=IE*IM
c: Xét ΔDMN và ΔDEF có
DM/DE=DN/DF
góc D chung
=>ΔDMN đồng dạng với ΔDEF
=>MN/EF=DM/DE=1/căn 2
=>(MN/EF)^2=1/2
Đúng 1
Bình luận (0)
Cho tam giác DEF có
D
^
80
o
các đường phân giác EM và FN cắt nhau tại S ta có: A.
E
D
S
^
40
o
.
B.
E
D
S
^
160
o
.
C. ...
Đọc tiếp
Cho tam giác DEF có D ^ = 80 o các đường phân giác EM và FN cắt nhau tại S ta có:
A. E D S ^ = 40 o .
B. E D S ^ = 160 o .
C. SD = SE = SF.
D. S E = 2 3 E M .
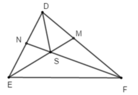
+ Vì S là giao điểm của hai đường phân giác EM và FN của tam giác DEF
Suy ra S là giao điểm của ba đường phân giác trong tam giác DEF
Nên DS là tia phân giác của góc EDF ⇒ E D S ^ = 1 2 E D F ^ = 1 2 .80 ° = 40 °
Do đó A đúng, B sai
+ S là giao của ba đường phân giác nên S cách đều ba cạnh của tam giác DEF nên C sai
+ S E = 2 3 E M là sai vì tính chất này chỉ có khi S là trọng tâm tam giác DEF và EM là trung tuyến nên D sai.
Chọn đáp án A
Đúng 0
Bình luận (0)
Cho tam giác DEF cân tại D. Phân giác góc E và góc F cắt cạnh DF và DE lần lượt ở M và N. EM cắt FN ở I a) chứng minh tam giác DEF cân tại D b)tam giác ENF=∆FME c)DI là phân giác góc I
Cho tam giác DEF cân tại D. Phân giác góc E và góc F cắt cạnh DF và DE lần lượt ở M và N. EM cắt FN ở I.
cho tam giác DEF ( DE=DF) . Gọi M và N lần lượt là trung điểm của DE và DF.
a) Chúng minh EM=FN và góc DEM =góc DFN
b) EM cắt FN tại K .C/M KE = KF
C) C/m DK là tia phân giác của góc EDF và DK đi qua trung điểm H của EF
a. vì tam giác DEF cân => DE=DF=>1/2DE=1/2DF=>DM=DN
Xét 2 tam giác DEM và tam giác DFNcó
DE=DF(gt)
góc D chung
DM=DN (cmt)
=>tam giác DEM = tam giác DFN(c,g,c)
=> EM=FN(cạnh tương ứng)
b. Vì góc DEM=góc DFN (cmt)
góc DEF =góc DEF (suy từ giả thuyết)
=>DEF - DEM = DFE - DFN => KEF = KFE
=> tam giác KEF cân
=> KE=KF
c. xét 2 tam giác : tam giác DKE và tam giácDKF
DE=DF (gt)
DK chung
KE=KF (cmt)
tam giác DKE =tam giác DKF (c.c.c)
=> góc EDK = góc FDK
kéo dài DK và và két EF tại H'
xét 2 tam giác tam giác DH'Evà tam giác DH'F
DE=DF
EDH'=FDH'
DH' chung
=> tam giác DH'E= tam giác DH'F
=>H'E =H'F(c.t.ư)
=> H và H' trùng nhau
=>Dk đi qua H
Đúng 0
Bình luận (0)
Cho tam giác DEF có DE=5cm, DF=9cm, DI là đường phân giác ( I thuộc EF ). Kẻ EM, FN vuông góc với DI. Qua trung điểm K của EF kẻ đường thẳng song song với DI cắt DF tại H, cắt ED tại C. Chứng minh EC=FH.
Xem chi tiết
???????????????????????????????????????????????????
bạn vẽ hình ra đi
Xem thêm câu trả lời
Cho tam giác DEF có 2 đường cao EM và FN cắt nhau tại I.Chứng minh rằng:4 điểm D,M,I,N cùng thuộc 1 đường tròn
Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc một đường tròn
Đúng 1
Bình luận (1)



