Cho ABC nhọn có 0 A = 60 ˆ , các đường cao là BE và CF. Chứng minh: ABC ~ AEF và SABC = 4SAEF
KL
Những câu hỏi liên quan
Cho tam giác nhọn ABC , các đường cao BE và CF a, chứng minh tam giác AEB đồng dạng với tam giác AFC. Từ đó suy ra AF. AB=AE.AC b, chứng minh góc AEF=ABC c, nếu tam giác ABC có có góc A=60°. Chứng minh rằng SABC=4SAEF
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra:
A
F
.
A
B
A
E
.
A
C
b) Chứng minh
∠
A
E
F
∠
A
B
C
c) Cho
A
E
3
c
m
,...
Đọc tiếp
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: A F . A B = A E . A C
b) Chứng minh ∠ A E F = ∠ A B C
c) Cho A E = 3 c m , A B = 6 c m . Chứng minh rằng S A B C = 4 S A E F
d) Chứng minh A F F B . B D D C . C E E A = 1
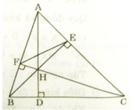
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
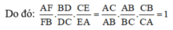
Đúng 4
Bình luận (0)
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại h
a) Chứng minh △AEB đồng dạng △AFC. Từ đó suy ra AF.AB=AE.AC
b) Chứng minh: góc AEF=góc ABC
c) Cho AE= 3cm, AB=6cm. Chứng minh rằng SABC= 4SAEF
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: AE/AF=AB/AC
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
c: ΔAEF đồng dạng với ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\dfrac{1}{4}\)
=>\(S_{ABC}=4\cdot S_{AEF}\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, các đường cao AD,BE,CF cắt nhau tại H
a) Chứng minh tam giác AEB đồng dạng với tam giác AFC. Từ đó suy ra AF.AB=AE.AC
b) Chứng minh: góc AEF= góc ABC
c) Cho AE=3cm, AB=6cm. Chứng minh rằng Sabc=4Saef.
làm hộ mình cám ơn các bạn nhiều
a) Xét \(\Delta AEB\) và \(\Delta AFC\) có:
\(\widehat{AEB}=\widehat{AFC}=90^0\)
\(\widehat{A}\) chung
suy ra: \(\Delta AEB~\Delta AFC\) (g.g)
\(\Rightarrow\)\(\frac{AE}{AF}=\frac{AB}{AC}\) \(\Rightarrow\)\(AF.AB=AE.AC\)
b) \(\frac{AE}{AF}=\frac{AB}{AC}\)\(\Rightarrow\)\(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét \(\Delta AEF\)và \(\Delta ABC\) có:
\(\frac{AE}{AB}=\frac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
suy ra: \(\Delta AEF~\Delta ABC\) (c.g.c)
\(\Rightarrow\) \(\widehat{AEF}=\widehat{ABC}\)
c) \(\Delta AEF~\Delta ABC\)
\(\Rightarrow\)\(\frac{S_{ABC}}{S_{AEF}}=\left(\frac{AB}{AE}\right)^2=\left(\frac{3}{6}\right)^2=\frac{1}{4}\)
\(\Rightarrow\)\(S_{ABC}=4S_{AEF}\)
Đúng 1
Bình luận (1)
Gửi các bạn lời giải 1 bài tương tự
https://youtu.be/mjiZSkISHgA
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, đường cao BE, CF. Gọi SAEF, SABC lần lượt là diện tích của tam giác AEF và tam giác ABC. Chứng minh SAEF/SABC =1-sin2A
Xét tam giác AEF và tam giác ABC có:
A chung
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(=cosA\right)\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2A=1-sin^2A\)
Đúng 0
Bình luận (0)
\(1-\sin^2A=\cos^2A=\dfrac{AF^2}{AC^2}\left(1\right)\)
Ta có \(\widehat{AEB}=\widehat{AFC}=90^0\Rightarrow\Delta AEB\sim\Delta AFC\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\\ \Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AF}{AC}\right)^2=\dfrac{AF^2}{AC^2}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC các đường cao AD, BE, CF cắt nhau đang cần gấp tại H a/Chứng minh tam giác AEB đồng dạng với TAM GIAC AFC. Từ đó suy ra AF.AB = AE. AC b/Cho AE=3cm, AB=6cm. Chứng minh rằng SABc =4SAEF.
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF;AE/AB=AF/AC
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng vói ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ABC}=4\cdot S_{AEF}\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, các đường cao AD, BE, CF
a. Chứng minh đồng dạng với .
b. Chứng minh AF.AB = AE. AC
c. Chứng minh: ΔAEF = ΔABC
d. Cho AE = 3cm, AB= 6cm. Chứng minh rằng SABC = 4SAEF
b) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AF\cdot AB=AE\cdot AC\)
c: Ta có: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)
Đúng 0
Bình luận (0)
Cho tam giác $ABC$ có ba góc nhọn, $\hat{A}={60}^\circ$. Kẻ hai đường cao $BE$ và $CF$.
a) Chứng minh $\Delta AEF\backsim\Delta ABC$;
b) Cho $EF=5cm$, tính $BC$.
c) Cho $S_{ABC}=100 cm^2$.Tính $S_{AEF}$.
hứng minh được , từ đó có \dfrac{AE}{AB} = \dfrac{AF}{AC}t.AE phần AB=AF phần AC
Ta có: (g.c.g)
b, từ câu a) suy ra EF phần BC=AE phần AB=cos A=cos60 độ =1 phần 2
=> BC=10cm
c) Saef phần Sabc=(AE phần AB)^2=cos^2 A=1 phần 4 => SAEF =1 phần 4 SABC=25cm^2
a)xét tam giác AEB và tam giác AFC có:
Góc A chung
góc AEB=góc AFC=90 độ(gt)
=> tam giác AEB đồng dạng với tam giác ABC (g.g)
=> \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
=> tam giác AEF đồng dạng với tam giác ABC (g.c.g)
b) theo a => \(\dfrac{EF}{BC}=\dfrac{AE}{AB}=cosA=cos60^0=\dfrac{1}{2}\)
=> Bc=10cm
c)\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2=\dfrac{1}{4}\)=>\(S_{AEF}=\dfrac{1}{4}S_{ABC}=25cm^2\)
Xem thêm câu trả lời
Bài 6: Cho hình thang cân ABCD ( AB//CD) có ˆ70oDa) Tính số đo các góc ˆ; ˆˆ;BCAb) Kẻ đường cao AH và BK của hình thang. Chứng minh DH CKBài 7: Cho tam giác ABC cân tại A. kẻ phân giác BE, CF của các góc B và C.a) Chứng minh tam giác AEF cânb) Chứng minh ∆ BFC ∆CEBc) Chứng minh BFEC là hình thang cânBài 8: Cho MNK cân tại M có đường phân giác MH. Gọi I là một điểm nằm giữa M và H. Tia KI cắt MN tạiA, tia NI cắt MK tại B.a. Chứng minh ABKN là hình thang cân.b. Chứng minh MI vừa là đường trun...
Đọc tiếp
Bài 6: Cho hình thang cân ABCD ( AB//CD) có ˆ
70oD
a) Tính số đo các góc ˆ
; ˆˆ
;BCA
b) Kẻ đường cao AH và BK của hình thang. Chứng minh DH = CK
Bài 7: Cho tam giác ABC cân tại A. kẻ phân giác BE, CF của các góc B và C.
a) Chứng minh tam giác AEF cân
b) Chứng minh ∆ BFC = ∆CEB
c) Chứng minh BFEC là hình thang cân
Bài 8: Cho MNK cân tại M có đường phân giác MH. Gọi I là một điểm nằm giữa M và H. Tia KI cắt MN tại
A, tia NI cắt MK tại B.
a. Chứng minh ABKN là hình thang cân.
b. Chứng minh MI vừa là đường trung trực của AB vừa là đường trung trực của KN.
\(7,\)
\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân\right)\\\widehat{B_1}=\widehat{C_1}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AFC=\Delta AEB\left(g.c.g\right)\\ \Rightarrow AF=AE\Rightarrow\Delta AFE.cân.tại.A\)
\(b,\left\{{}\begin{matrix}\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân\right)\\BC.chung\\\widehat{B_2}=\widehat{C_2}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\end{matrix}\right.\Rightarrow\Delta BFC=\Delta CEB\left(g.c.g\right)\)
\(c,\widehat{F_1}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta AEF.cân\right);\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta ABC.cân\right)\\ \Rightarrow\widehat{F_1}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị nên \(EF//BC\Rightarrow BEFC\) là hình thang
Mà \(\widehat{ABC}=\widehat{ACB}\left(GT\right)\)
Vậy \(BEFC\) là hình thang cân
Đúng 2
Bình luận (1)






