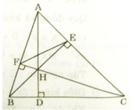
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
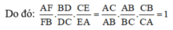

a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
Cho tam giác ABC có các đường trung tuyến AD, BE và CF cắt nhau tại trọng
tâm G (D ∈ BC, E ∈ AC, F ∈ AB). Trên tia đối của tia F C lấy điểm N sao cho F N = F C.
a) Chứng minh rằng ∆AF N = ∆BF C. Từ đó, hãy suy ra rằng AN = BC.
b) Lấy K ∈ NF sao cho FK = F G. Chứng minh rằng ∆AFK = ∆BF G. Từ đó, hãy suy ra rằng
AD < BE + CF.
c) Giả sử AGB \≤ 900
. Chứng minh rằng F A = F B ≤ F G. Từ đó, hãy chứng tỏ rằng AC + BC >
3AB.
Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác trong BD.
a) Chứng minh tam giác BAH đồng dạng với tam giac BCA. Suy ra AH.BC=AB.AC
b) Chứng minh DA/DC=AH/AC
c) Qua C vẽ đường thẳng d song song với BD, từ B kẻ BE _|_d (E thuộc d), đường thẳng BE cắt AC tại F. Chứng minh DA.FC=DC.FA
d) Chứng minh tam giác ABE đồng dạng với tam giác BDC.
Hình thang ABCD(AB//CD) có AB=a, BC=b, CD=c, AD=d. các tia phân giác góc A và D cắt nhau tại E. các tia phân giác góc B và góc C cắt nhau tại F. gọi M, N là trung điểm của AD, BC. a. Chứng minh tam giác AED vuông. b. Chứng minh rằng nếu E trùng với F thì a+b=c+d.
Tam giác ABC vuông tại A (AB < AC). Vẽ đường cao AH. Lấy D đối xứng với B qua H.
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA
b) Qua C vẽ đường thẳng vuông góc với tia AD cắt AD tại E. Chứng minh rằng AH.CD = CE.AD
c) Chứng minh tam giác HDE đồng dạng với tam giác ADC.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích tam giác DEC
e) AH cắt CE tại F. Chứng minh ABFD là hình thoi.
Cho hình bình hành ABCD có góc A = 60 độ , AD = 2AB, gọi M là trung điểm AD , N là trung điểm của BC . a) chứng minh tứ giác MNCD là hình thoi . b) từ C kẻ đường thẳng vuông góc với MN tại E , cắt AB tại F chứng minh E là trung điểm của CF . c) chứng minh tam giác MCF đều . d) chứng minh ba F,N,D điểm thẳng hàng
Cho hình bình hành ABCD có góc A = 60 độ , AD = 2AB, gọi M là trung điểm AD , N là trung điểm của BC . a) chứng minh tứ giác MNCD là hình thoi . b) từ C kẻ đường thẳng vuông góc với MN tại E , cắt AB tại F chứng minh E là trung điểm của CF . c) chứng minh tam giác MCF đều . d) chứng minh ba F,N,D điểm thẳng hàng
từ 3 đỉnh A,B,C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt cạnh BC và các đường thẳng CA, AB tại D,E,F chứng minh rằng:
a. 1/AD=1/BE+1/CF
b. S DEF =2S ABC
Lưu ý S là diện tích nha
Cho hình bình hành ABCD có góc A = 60 độ , AD = 2AB, gọi M là trung điểm AD , N là trung điểm của BC .
a) chứng minh tứ giác MNCD là hình thoi .
b) từ C kẻ đường thẳng vuông góc với MN tại E , cắt AB tại F chứng minh E là trung điểm của CF .
c) chứng minh tam giác MCF đều .
d) chứng minh ba F,N,D điểm thẳng hàng
Giải câu (c,d)
Cho tam giác ABC có AB<AC, D nằm giữa A và C sao cho góc ABD = góc ACB. a, Chứng minh: tam giác ADB đồng dạng với tam giác ABC, từ đó suy ra AB^2 = AC.AD ; b, Biết diện tích tam giác ABC= 16cm^2, AB= 8cm.Tính diện tích tam giác ABD ; c, Phân giác của góc A cắt BC tại E, cắt BD tại F. Chứng minh rằng FD/FB = EB/ EC