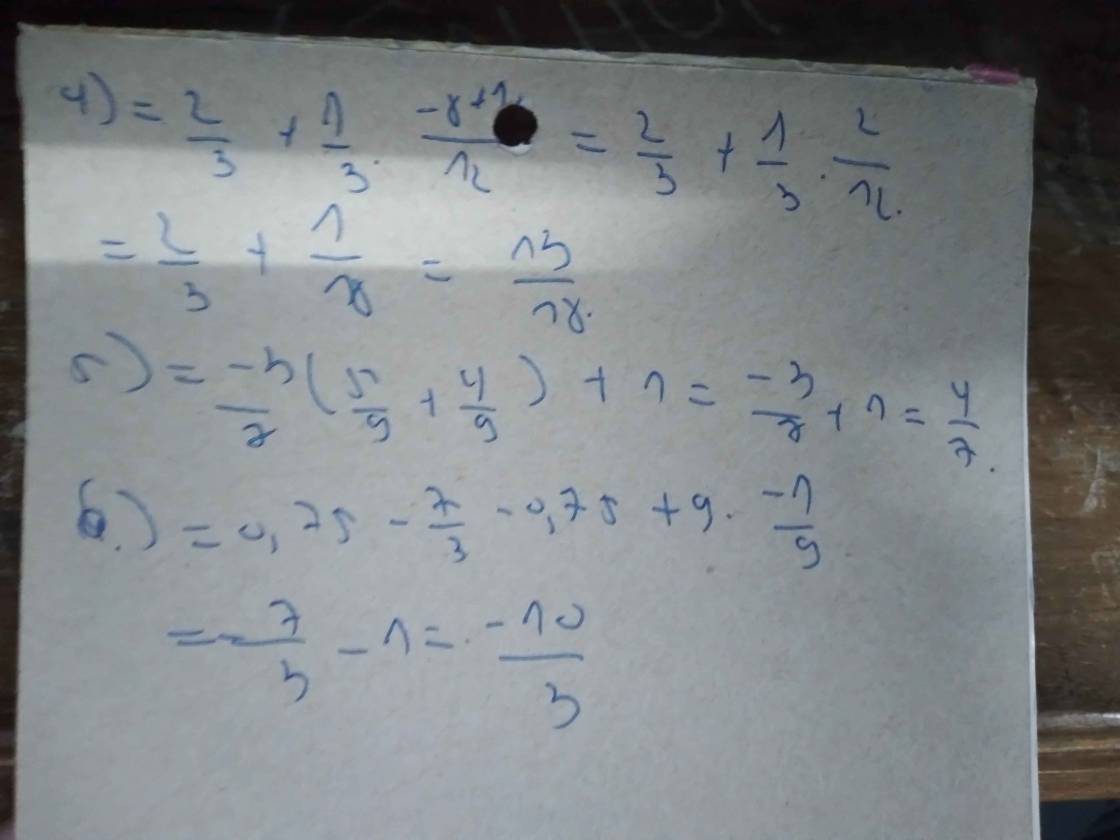1) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

Ta có: \(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{4}{x^2-1}\)

\(\Leftrightarrow\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)

Suy ra: \(x^2+2x+1-\left(x^2-2x+1\right)=4\)

\(\Leftrightarrow x^2+2x+1-x^2+2x-1=4\)

\(\Leftrightarrow4x=4\)

hay x=1(loại)

Vậy: \(S=\varnothing\)

2) ĐKXĐ: \(x\notin\left\{2;-2\right\}\)

Ta có: \(\dfrac{x+2}{x-2}+\dfrac{x}{x+2}=2\)

\(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2\left(x^2-4\right)}{\left(x-2\right)\left(x+2\right)}\)

Suy ra: \(x^2+4x+4+x^2-2x=2x^2-8\)

\(\Leftrightarrow2x^2+2x+4-2x^2-8=0\)

\(\Leftrightarrow2x-4=0\)

\(\Leftrightarrow2x=4\)

hay x=2(loại)

Vậy: \(S=\varnothing\)

a: x*3/4=1/5

=>x=1/5:3/4=1/5*4/3=4/15

b: x*3/7=2/5

=>x=2/5:3/7=2/5*7/3=14/15

c: 1/3+2/9=2/12x

=>1/6x=3/9+2/9=5/9

=>x=5/9*6=30/9=10/3

d: 4/15*x-2/3=1/5

=>4/15*x=2/3+1/5=10/15+3/15=13/15

=>4x=13

=>x=13/4

e: x:1/7=2/3

=>x=2/3*1/7=2/21

f: 1/9:x=7/3

=>x=1/9:7/3=1/9*3/7=3/63=1/21

j: 1/4+5/12=8/3:x

=>8/3:x=3/12+5/12=8/12=2/3

=>x=4

h: =>7/4:x=1/5+1/2=7/10

=>x=7/4:7/10=10/4=5/2

a) \(x=\dfrac{25}{72}\)

b)\(x=-\dfrac{1}{4}\)

  \(x=\dfrac{3}{2}\)

c)\(x=\dfrac{5}{4}\) hoặc

  x \(=\dfrac{8}{5}\)

d và e chịu vì mk kg giỏi lắm về mũ 

f)\(x=-2\)

G)\(x=-\dfrac{5}{12}\)

.

__  |

Let's solve each equation step by step:

Squaring both sides of the equation, we get:
x^2 - 6x + 9 = (3 - x)^2
x^2 - 6x + 9 = 9 - 6x + x^2

The x^2 terms cancel out, and we are left with:
-6x = -6x

This equation is true for any value of x. Therefore, there are infinitely many solutions.

Moving all terms to one side of the equation, we get:
x^2 - (1/2)x - x + 3/2 - 1/16 = 0
x^2 - (3/2)x + 29/16 = 0

To solve this quadratic equation, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)

In this case, a = 1, b = -3/2, and c = 29/16. Plugging in these values, we get:
x = (3/2 ± √((-3/2)^2 - 4(1)(29/16))) / (2(1))
x = (3/2 ± √(9/4 - 29/4)) / 2
x = (3/2 ± √(-20/4)) / 2
x = (3/2 ± √(-5)) / 2

Since the square root of a negative number is not a real number, this equation has no real solutions.

Squaring both sides of the equation, we get:
(x - 2)(x - 1) = (x - 1) - 2√(x - 1) + 1
x^2 - 3x + 2 = x - 1 - 2√(x - 1) + 1
x^2 - 4x + 2 = -2√(x - 1)

Squaring both sides again, we get:
(x^2 - 4x + 2)^2 = (-2√(x - 1))^2
x^4 - 8x^3 + 20x^2 - 16x + 4 = 4(x - 1)
x^4 - 8x^3 + 20x^2 - 16x + 4 = 4x - 4

Rearranging terms, we have:
x^4 - 8x^3 + 20x^2 - 20x + 8 = 0

This equation does not have a simple solution and requires further calculations or approximation methods to find the solutions.

Simplifying the left side of the equation, we get:
3 - 4√5 - √5 = -2
-√5 - 5 = -2
-√5 = 3

This equation is not true since the square root of a number cannot be negative.

Therefore, the given equations either have infinitely many solutions or no real solutions.

a: =91/105+60/105-101/105

=50/105=10/21

c: \(\dfrac{3}{4}\cdot\dfrac{5}{2}\cdot\dfrac{7}{6}=\dfrac{3}{6}\cdot\dfrac{7}{2}\cdot\dfrac{5}{4}=\dfrac{1}{2}\cdot\dfrac{7}{2}\cdot\dfrac{5}{4}=\dfrac{35}{16}\)

d: =2-2/9

=18/9-2/9

=16/9

e: =24/36-9/36+8/36

=23/36

g: =5/2+1/2

=3

Câu 1 : 

a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)

\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)

\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)

Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)

tương tự 

\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)

\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)

\(< =>95-24x+40=6-4x-15x+5\)

\(< =>-24x+135=-19x+11\)

\(< =>5x=135-11=124\)

\(< =>x=\frac{124}{5}\)

\(\frac{\left(x-2\right).3}{2}+3+\frac{\left(x-3\right).5}{3}+5+\frac{\left(x-5\right).2}{5}+2=10\)

\(< =>\frac{\left(x-2\right).3.15}{30}+\frac{\left(x-3\right).5.10}{30}+\frac{\left(x-5\right).2.6}{30}=10-2-3-5\)

\(< =>\frac{\left(x-2\right).45+\left(x-3\right).50+\left(x-5\right).12}{30}=0\)

\(< =>45x-90+50x-150+12x-60=0\)

\(< =>107x-300=0< =>x=\frac{300}{107}\)

đéo bt

Dài thế trời!!!

1) 1/3 x 1/2 x 3/7 = 1/6 x 3/7 = 1/14

2) 5/4 x 1/3 + 1/7 = 5/12 + 1/7 = 47/84

3) 8 x (8/9 - 2/3) = 8 x 2/9 = 16/9

4) 5/6 x 48/20 x 1/2 = 2 x 1/2 = 1

5) (2/5 + 3/4) x 8 = 23/20 x 8 = 46/5

6) 10 x (1/2 - 1/5) = 10 x 3/10 = 3