Tất cả các giá trị của tham số m để hàm số f(x) =1/ (\/2x*2-3x+3m-2) có tập xác định D=R
TT
Những câu hỏi liên quan
Cho hàm số y=\(\sqrt{x+m-1}+\sqrt{m-3x}\).Tìm tất cả các giá trị nguyên của tham số m để hàm số đã cho có tập xác định là R.
Tìm tất cả các giá trị thực của tham số m để hàm số y= log( x2- 2x- m+ 1) có tập xác định là R
A. m≥ 0.
B. m<0
C. m ≤ 2.
D. m> 2.
Chọn B
Để hàm số đã cho có tập xác định là R khi và chỉ khi : x2- 2x-m+ 1> 0 với mọi x
Hay
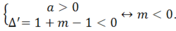
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
log
(
x
2
-
2
x
-
m
+
1
)
có tập xác định là R: A.
m
≥
0
B. m 0 C.
m
≤
2
D. m 2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 x - m + 1 ) có tập xác định là R:
A. m ≥ 0
B. m < 0
C. m ≤ 2
D. m > 2
Cho hàm số yf(x) xác định, liên tục trên R{1} và có bảng biến thiên như sauTìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)m có nghiệm lớn hơn 2 A.
(
-
∞
;
1
)
B. (3;4) C.
(
1
;
+
∞
)
D.
(
4
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như sau
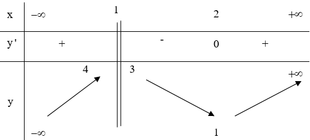
Tìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)=m có nghiệm lớn hơn 2
A. ( - ∞ ; 1 )
B. (3;4)
C. ( 1 ; + ∞ )
D. ( 4 ; + ∞ )
Cho hàm số y=\(\sqrt{x^4-x^2+1+mx\sqrt{2x^4+2}}.\) . Tìm tất cả các giá trị của tham số m để hàm số có tập xác định là tập số thực R. GIẢI GIÚP MÌNH VỚI!!
tìm tập tất cả các giá trị của tham số m để hàm số y= -1/3x^3-(m-2)x^2+(m-2)x+m luôn nghịch biến trên tập xác định
\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
l
n
x
2
-
2
m
x
+
4
có tập xác định D R A. -2 m 2 B. m 2 C.
-
2
≤
m
≤
2
D. m 2 hoặc m -2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = l n x 2 - 2 m x + 4 có tập xác định D = R
A. -2 < m < 2
B. m < 2
C. - 2 ≤ m ≤ 2
D. m > 2 hoặc m < -2
Cho hàm số yf(x) xác định, liên tục trên R và có bảng biến thiên như sau:Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1m có đúng 2 nghiệm A. -2 m -1 B. m 0, m -1 C. m -2, m -1 D. m -2, m ≥ -1
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1=m có đúng 2 nghiệm
A. -2 < m < -1
B. m > 0, m = -1
C. m = -2, m > -1
D. m = -2, m ≥ -1
Chọn đáp án C
Phương pháp
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m song song với trục hoành.
Cách giải
Ta có:
![]()
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m+1 song song với trục hoành.
Từ BBT ta thấy để phương trình f(x)-1=m có đúng 2 nghiệm thì
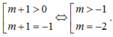
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m trên đoạn
[-2020; 2020] để hàm số f(x) = \(\dfrac{\sqrt{x^2-2x+3}}{x^2-2x+m-1}\) có tập xác định là R?
Tìm tất cả các giá trị thực của tham số m để hàm số
y
l
n
(
x
2
-
2
m
x
+
4
)
có tập xác định D R A.-2 m 2 B. m 2 C.
-
2
≤
m
≤
2
D. m 2 hoặc m -2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = l n ( x 2 - 2 m x + 4 ) có tập xác định D = R
A.-2 < m < 2
B. m < 2
C. - 2 ≤ m ≤ 2
D. m > 2 hoặc m < -2



