Giúp mik bài này gấp với 
TL
Những câu hỏi liên quan
giúp mik bài này với ạ, mik cần gấp 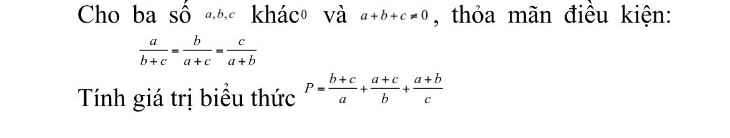

giúp mik bài này với mik đang cần gấp
\(\left(xy+3\right)^2+\left(x+y\right)^2=8\)
\(\Leftrightarrow x^2y^2+x^2+y^2+1=-8xy\)
\(\dfrac{x}{x^2+1}+\dfrac{y}{y^2+1}=-\dfrac{1}{4}\Leftrightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{x^2y^2+x^2+y^2+1}=-\dfrac{1}{4}\)
\(\Rightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{-8xy}=-\dfrac{1}{4}\)
\(\Rightarrow\left(xy+1\right)\left(x+y\right)=2xy\)
\(\Rightarrow x+y=\dfrac{2xy}{xy+1}\)
Thế vào pt ban đầu:
\(\left(xy+3\right)^2+\left(\dfrac{2xy}{xy+1}\right)^2=8\)
Đặt \(xy+1=t\Rightarrow\left(t+2\right)^2+4\left(\dfrac{t-1}{t}\right)^2=8\)
\(\Rightarrow\left(t^2+2t\right)^2-4\left(t^2+2t\right)+4=0\)
\(\Leftrightarrow\left(t^2+2t-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1-\sqrt{3}\\t=-1+\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}xy=-2-\sqrt{3}\Rightarrow x+y=1+\sqrt{3}\\xy=-2+\sqrt{3}\Rightarrow x+y=1-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow x;y\) là nghiệm của: \(\left[{}\begin{matrix}X^2-\left(1+\sqrt{3}\right)X-2-\sqrt{3}=0\\X^2-\left(1-\sqrt{3}\right)X-2+\sqrt{3}=0\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 0
Bình luận (0)
 Giúp mik bài này với ạ, mik cần gấp! Mik cảm ơn!!
Giúp mik bài này với ạ, mik cần gấp! Mik cảm ơn!!
mn ơi giúp mik bài này với, mik cần gấp ! 

giúp mik 3 bài này với ạ, mik cần gấp!!!
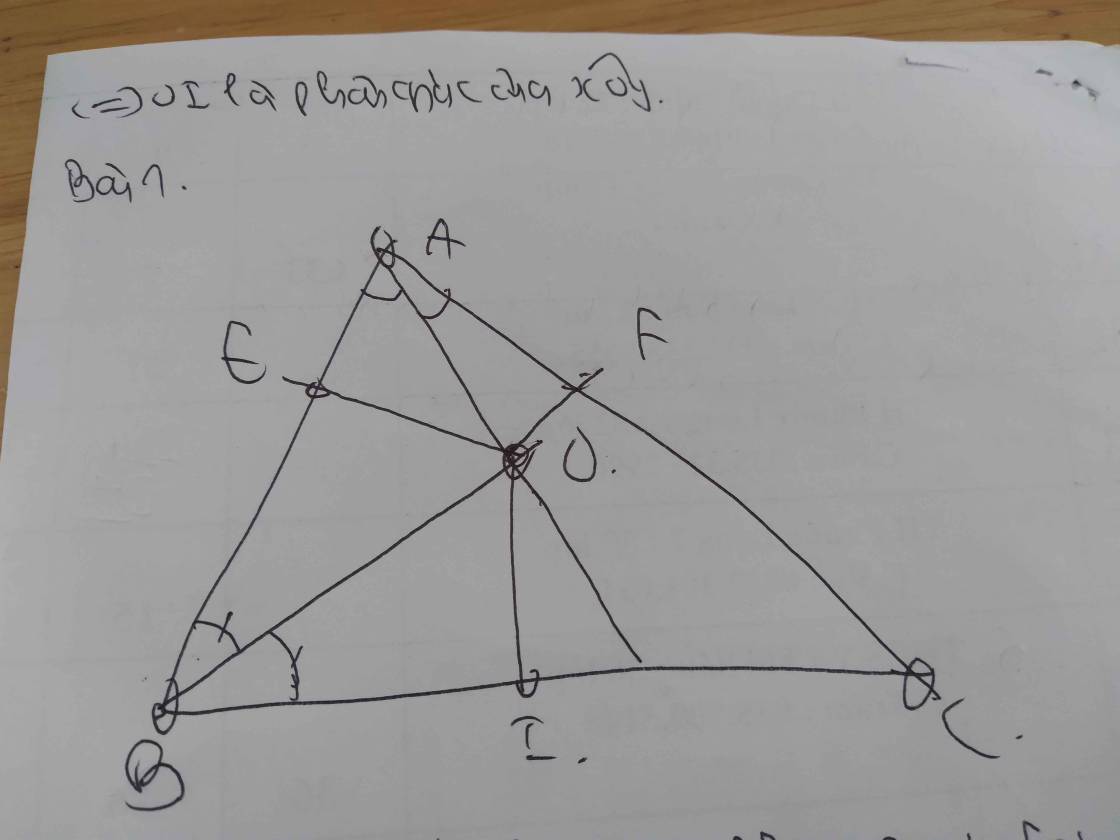
Bài 1
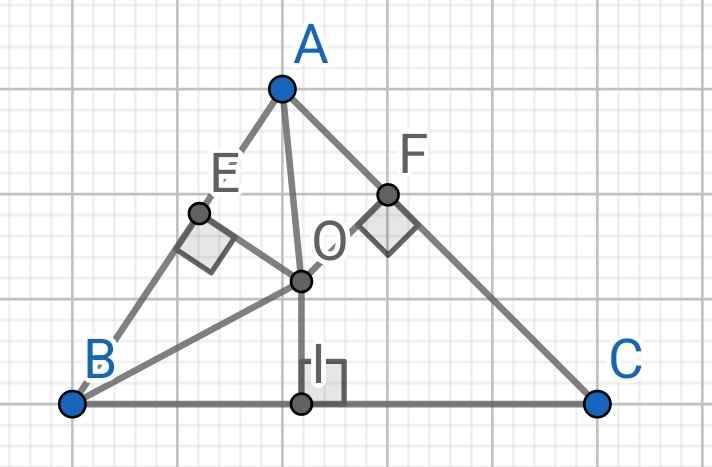 Do BO là tia phân giác của ∠ABC (gt)
Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
Đúng 2
Bình luận (0)
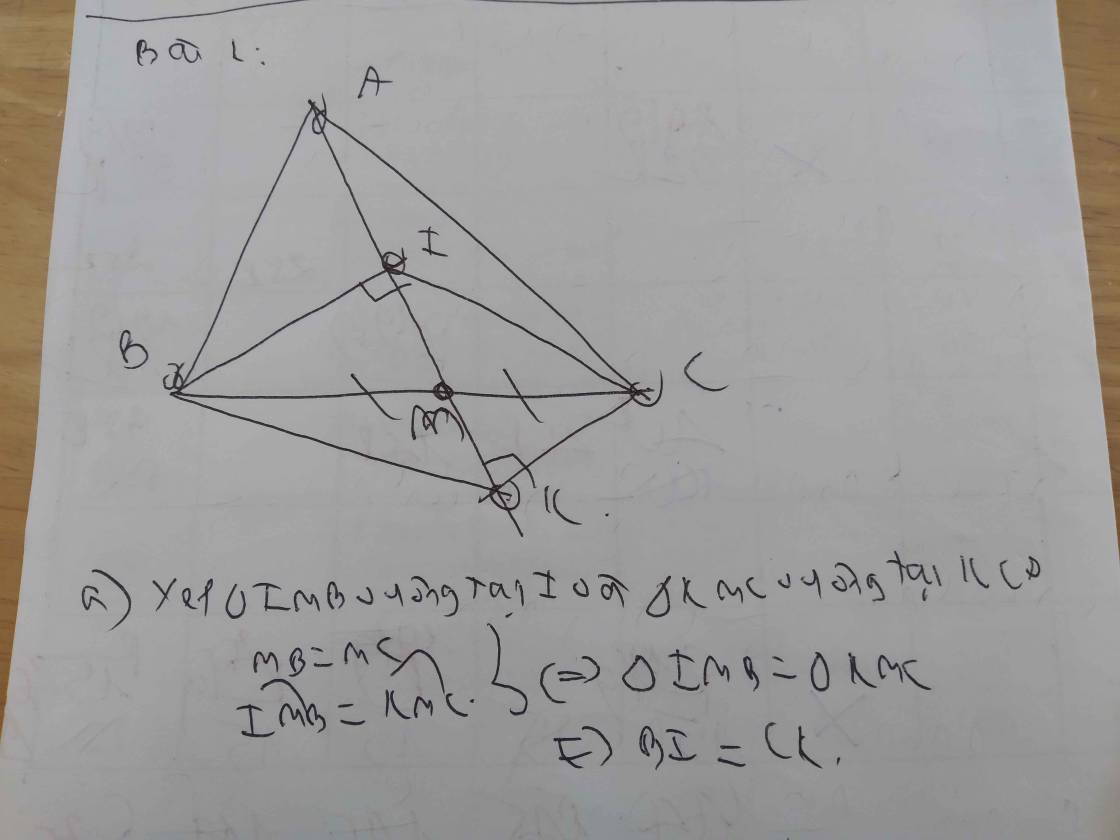
Bài 2
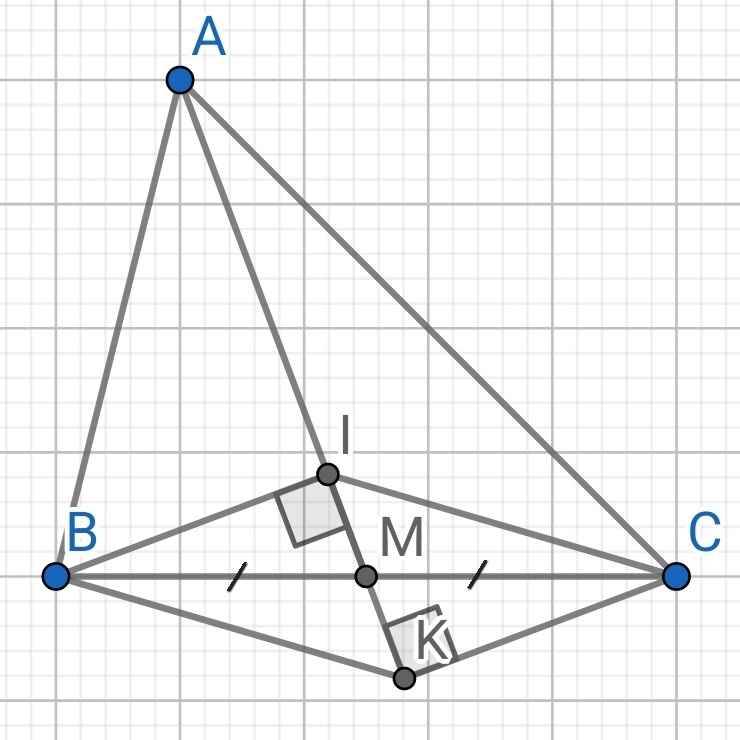 a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
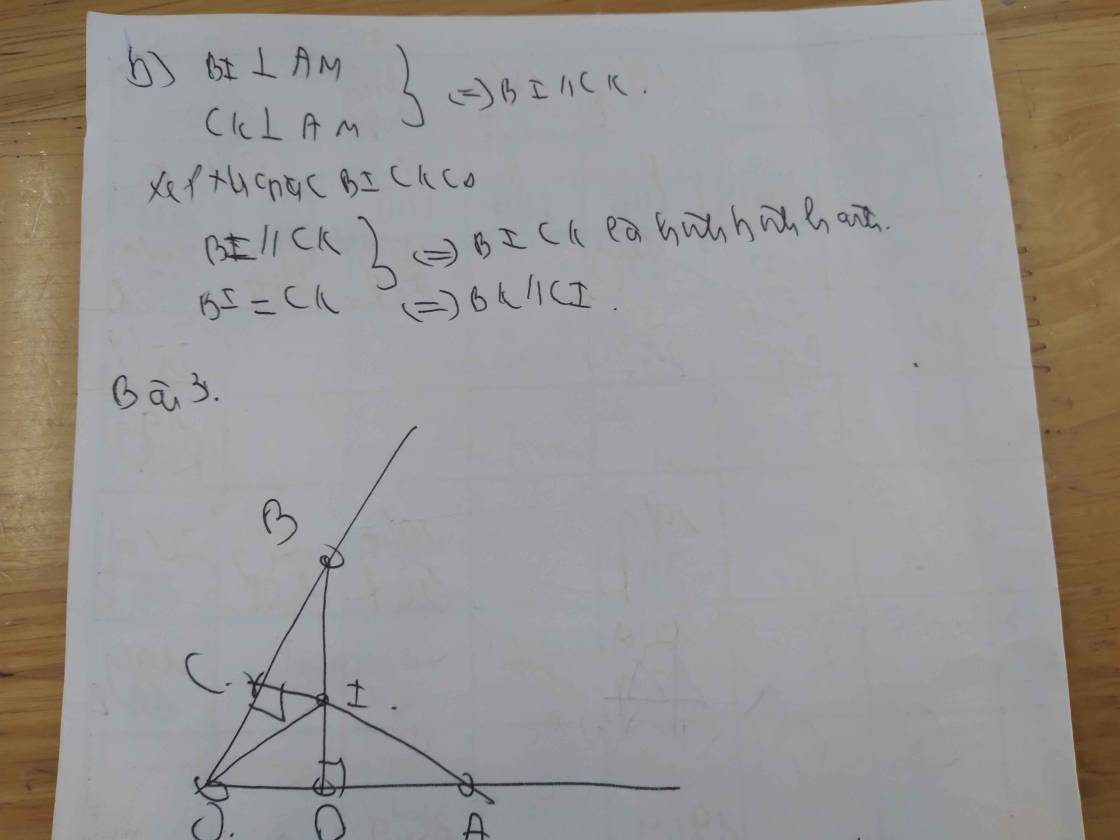
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI
Đúng 2
Bình luận (1)
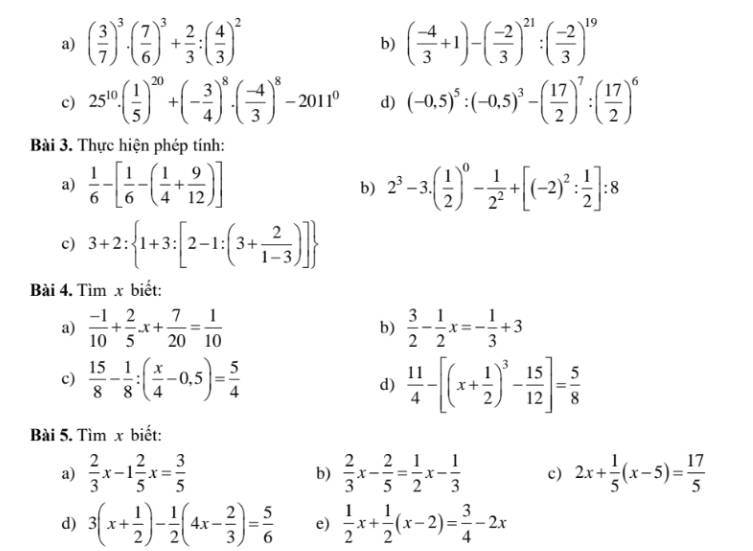
giúp mik mấy bài này với ạ mik đg cần gấp ạ
4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1
Đúng 0
Bình luận (0)
Các bạn giúp mik với bài này hơi khó với lại mik cần gấp pls );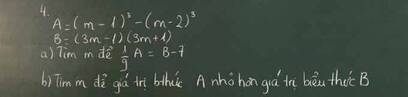
\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
giúp mik mấy bài này với mik cần rất gấp trước 3h nha
Đọc tiếp




giúp mik mấy bài này với mik cần rất gấp trước 3h nha
Bạn nào giúp mik 3 bài này với
Mik cảm ơn ạ
Vì mik đag gấp á nên mong các bạn giúp mik vs

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
Đúng 0
Bình luận (0)