1: \(MTC=2\left(x-y\right)\left(x+y\right)\)

\(\dfrac{x-y}{2x^2-4xy+2y^2}=\dfrac{x-y}{2\left(x-y\right)^2}=\dfrac{1}{2\left(x-y\right)}=\dfrac{1\cdot\left(x+y\right)}{2\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{2\left(x-y\right)\left(x+y\right)}\)

\(\dfrac{x+y}{2x^2+4xy+2y^2}\)

\(=\dfrac{x+y}{2\left(x^2+2xy+y^2\right)}\)

\(=\dfrac{x+y}{2\left(x+y\right)^2}=\dfrac{1}{2\left(x+y\right)}=\dfrac{x-y}{2\left(x+y\right)\left(x-y\right)}\)

\(\dfrac{1}{x^2-y^2}=\dfrac{2}{2\left(x^2-y^2\right)}=\dfrac{2}{2\left(x-y\right)\left(x+y\right)}\)

2: \(\dfrac{1}{x^2+8x+15}=\dfrac{1}{\left(x+3\right)\left(x+5\right)}=\dfrac{x+3}{\left(x+3\right)^2\cdot\left(x+5\right)}\)

\(\dfrac{1}{x^2+6x+9}=\dfrac{1}{\left(x+3\right)^2}=\dfrac{x+5}{\left(x+3\right)^2\cdot\left(x+5\right)}\)

3: \(\dfrac{1}{\left(a-b\right)\left(b-c\right)}=\dfrac{1\cdot\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=\dfrac{a-c}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)

\(\dfrac{1}{\left(c-b\right)\left(c-a\right)}=\dfrac{1}{\left(b-c\right)\left(a-c\right)}=\dfrac{a-b}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)

\(\dfrac{1}{\left(b-a\right)\left(a-c\right)}=\dfrac{-1}{\left(a-b\right)\left(a-c\right)}=\dfrac{-\left(b-c\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)

`@` `\text {Ans}`

`\downarrow`

`a)`

`3x(4x-1) - 2x(6x-3) = 30`

`=> 12x^2 - 3x - 12x^2 + 6x = 30`

`=> 3x = 30`

`=> x = 30 \div 3`

`=> x=10`

Vậy, `x=10`

`b)`

`2x(3-2x) + 2x(2x-1) = 15`

`=> 6x- 4x^2 + 4x^2 - 2x = 15`

`=> 4x = 15`

`=> x = 15/4`

Vậy, `x=15/4`

`c)`

`(5x-2)(4x-1) + (10x+3)(2x-1) = 1`

`=> 5x(4x-1) - 2(4x-1) + 10x(2x-1) + 3(2x-1)=1`

`=> 20x^2-5x - 8x + 2 + 20x^2 - 10x +6x - 3 =1`

`=> 40x^2 -17x - 1 = 1`

`d)`

`(x+2)(x+2)-(x-3)(x+1)=9`

`=> x^2 + 2x + 2x + 4 - x^2 - x + 3x + 3=9`

`=> 6x + 7 =9`

`=> 6x = 2`

`=> x=2/6 =1/3`

Vậy, `x=1/3`

`e)`

`(4x+1)(6x-3) = 7 + (3x-2)(8x+9)`

`=> 24x^2 - 12x + 6x - 3 = 7 + (3x-2)(8x+9)`

`=> 24x^2 - 12x + 6x - 3 = 7 + 24x^2 +11x - 18`

`=> 24x^2 - 6x - 3 = 24x^2 + 18x -11`

`=> 24x^2 - 6x - 3 - 24x^2 + 18x + 11 = 0`

`=> 12x +8 = 0`

`=> 12x = -8`

`=> x= -8/12 = -2/3`

Vậy, `x=-2/3`

`g)`

`(10x+2)(4x- 1)- (8x -3)(5x+2) =14`

`=> 40x^2 - 10x + 8x - 2 - 40x^2 - 16x + 15x + 6 = 14`

`=> -3x + 4 =14`

`=> -3x = 10`

`=> x= - 10/3`

Vậy, `x=-10/3`

Hello các bạn còn đó ko?

a,

đoạn 9x-6-> 2x-6=0

=> x=3

b,6x^2+13x+5=6x^2-20x+6

33x=1

=>x=1/33

a) (x+1)(x+9)=(x+3)(x+5) 

<=>x^2+10x+9=x^2+8x+15

<=>x^2+10x+9-x^2-8x-15=0

<=>9x-6=0 phải là 2x - 6

<=>9x=6

<=>x=6/9=2/3 => S= 2/3

d) (3x+5)(2x+1)=(6x-2)(x-3)

<=>6x^2+13x+5=6x^2-16x+6 phải là 6x^2 - 20x + 6

<=>6x^2+13x+5-6x^2+16x-6=0

<=>29x-1=0

<=>29x=1

<=>x=1/29

a) \(\left(x+1\right)\left(x+9\right)=\left(x+3\right)\left(x+5\right)\)

\(\Leftrightarrow x^2+10x+9=x^2+8x+15\)

\(\Leftrightarrow x^2+10x+9-x^2-8x-15=0\)

\(\Leftrightarrow2x-6=0\)

\(\Leftrightarrow x=3\)

Vây tập nghiệm của phương trình là \(S=\left\{3\right\}\)

d) \(\left(3x+5\right)\left(2x+1\right)=\left(6x-2\right)\left(x-3\right)\)

\(\Leftrightarrow6x^2+13x+5=6x^2-20x+6\)

\(\Leftrightarrow6x^2+13x+5-6x^2+20x-6=0\)

\(\Leftrightarrow33x-1=0\)

\(\Leftrightarrow x=\frac{1}{33}\)

Vây tập nghiệm của phương trình là \(S=\left\{\frac{1}{33}\right\}\)

a) Tìm MTC:

\(\text{2x + 6 = 2(x + 3)}\)

\(\text{x2 – 9 = (x – 3)(x + 3)}\)

\(\text{MTC = 2(x – 3)(x + 3) = 2(x2 – 9)}\)

Nhân tử phụ:

\(\text{2(x – 3)(x + 3) : 2(x + 3) = x – 3}\)

\(\text{2(x – 3)(x + 3) : (x2 – 9) = 2}\)

Qui đồng:

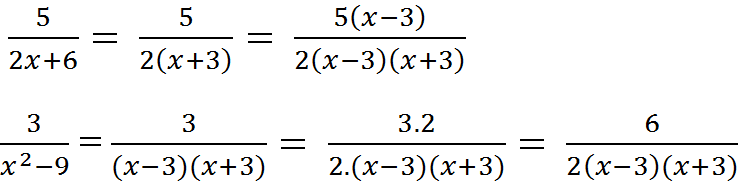
b) Tìm MTC:

a) = (x -1). (x + 1)

b) \(=\left(x+3\right)^2\)

c) \(=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)

d) \(=\left(4x\right)^2-2.4x.1+1=\left(4x-1\right)^2\)

\(a,\dfrac{7x-1}{2x^2+6x}=\dfrac{\left(7x-1\right)\left(x-3\right)}{2x\left(x+3\right)\left(x-3\right)}=\dfrac{7x^2-22x+3}{2x\left(x-3\right)\left(x+3\right)}\\ \dfrac{5-3x}{x^2-9}=\dfrac{2x\left(5-3x\right)}{2x\left(x-3\right)\left(x+3\right)}=\dfrac{10x-6x^2}{2x\left(x-3\right)\left(x+3\right)}\)

\(f,\dfrac{x^2-6x+9}{x^2-8x+15}\\ =\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x-5\right)}\\ =\dfrac{x-3}{x-5}\\ l,\dfrac{5xy+5x+3+3y}{10xy-15x-9+6y}\\ =\dfrac{5x\left(y+1\right)+3\left(y+1\right)}{5x\left(2y-3\right)+3\left(2y-3\right)}\\ =\dfrac{\left(y+1\right)\left(5x+3\right)}{\left(2y-3\right)\left(5y+3\right)}\\ =\dfrac{y+1}{2y-3}\)