Cho tam giác ABC và k là số thực cho trước. Tìm tập hợp những điểm M sao cho MA2 - MB2 = k
XO
Những câu hỏi liên quan
Cho tam giác ABC có AB = 22, BC = 19, CA = 13. Tìm tập hợp điểm M sao cho:
a) MA2 + MB2 + MC2 = k2b) AM2 + CM2 = BM2c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của BM nếu AM2 + CM2 = BM2
a, Gọi I là trọng tâm của ΔABC
⇒ \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
MA2 + MB2 + MC2 = k2
⇔ 3MI2 + 2\(\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+AB^2+AC^2+BC^2\) = k2
⇔ 3MI2 = k2 - 1014
⇔ MI = \(\sqrt{\dfrac{k-1014}{3}}\) = const
Vậy M thuộc \(\left(I;\sqrt{\dfrac{k-1014}{3}}\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC và số thực k 0; G là trọng tâm của tam giác ABC. Tập hợp các điểm M sao cho
M
A
→
+
M
B
→
+
M
C
→
k...
Đọc tiếp
Cho tam giác ABC và số thực k > 0; G là trọng tâm của tam giác ABC. Tập hợp các điểm M sao cho M A → + M B → + M C → = k là:
A. Đường tròn ngoại tiếp tam giác ABC
B. Đường tròn tâm G, bán kính k/3
C. Đường tròn tâm G, bán kính k
D. Đường tròn tâm G, bán kính 3k
Cho A(1; 2), B(-3; 1) và C(4; -2). Tìm tập hợp các điểm M sao cho MA2 + MB2= MC2
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm M thuộc cạnh AC ( M khác A, C ). Tìm tập hợp những điểm N trên cạnh BC sao cho tam giác ABC có diện tích bằng k lần diện tích tam giác MNC ( với k>1)
Cho tam giác đều ABC cạnh a.
a, Cho M là một điểm trên đường tròn ngoại tiếp tam giác ABC. Tính MA2 + MB2 + MC2 theo a.
b, Cho đường thẳng d tùy ý, tìm điểm N trên đường thẳng d sao cho NA2 + NB2 + NC2 nhỏ nhất.
a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
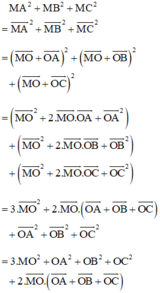
Lại có:
+ O là trọng tâm tam giác nên 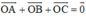
+ Bán kính đường tròn ngoại tiếp tam giác:
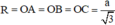
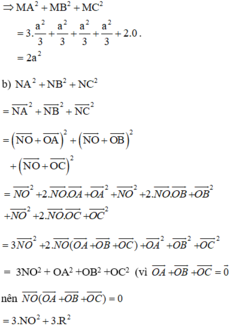
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
Đúng 0
Bình luận (0)
Trong không gian cho ba điểm A, B, C.
Tìm tập hợp các điểm M sao cho: M A 2 + 2 M B 2 - 2 M C 2 = k 2 , với k là hằng số
Ta có: M A 2 + 2 M B 2 - 2 M C 2 = k 2
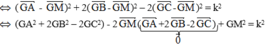

Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a . Tìm tập hợp M sao cho :
2 MA2 + MB2 = MC2 + MD2
Trong mặt phẳng cho trước hai điểm A, B và k là một số thực dương khác 1 cho trước. Tìm tập hợp tất cả các điểm M (của mặt phẳng) sao cho \(\frac{MA}{MB}=k\)
Ta có \(\frac{MA}{MB}=k\Leftrightarrow MA^2=k^2MB^2\Leftrightarrow\overrightarrow{MA^2}=k^2\overrightarrow{MB^2}\)
\(\Leftrightarrow\left(\overrightarrow{MA}-k\overrightarrow{MB}\right)\left(\overrightarrow{MA}+k\overrightarrow{MB}\right)=0\)
Gọi P, Q là các điểm thỏa mãn \(\overrightarrow{PA}.\overrightarrow{MQ}=0\Leftrightarrow MP\perp MQ\)
Từ đó suy ra tập hợp tất cả các điểm M cần tìm là đường tròn đường kính PQ
* Với k=1,quỹ tích cần tìm là đường trung trực (tương ứng mặt phẳng trung trực, với bài toàn trong không gian) của đoạn thẳng AB
* Đường tròn tìm được trong bài trên được gọi là đường tròn Apolonius
* Với bài toàn ở trong không gian, tương tự như vậy, ta cũng thu được quỹ tích là mặt cầu đường kính PQ, và mặt cầu đó cũng được gọi là mặt cầu Apolpnius
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại B và M thuộc miền trong tam giác sao cho góc BMC =135 độ. Chứng minh MA2=2.MB2+MC2
Trong không gian cho tam giác ABC đều cạnh bằng 2 cố định, M là điểm thỏa mãn điều kiện
M
A
2
+
M
B
2
+
M
C
2
12
Khẳng định nào sau đ...
Đọc tiếp
Trong không gian cho tam giác ABC đều cạnh bằng 2 cố định, M là điểm thỏa mãn điều kiện M A 2 + M B 2 + M C 2 = 12 Khẳng định nào sau đây đúng ?
A. Tập hợp các điểm M là một mặt cầu có bán kính R = 7
B. Tập hợp các điểm M là một mặt cầu có bán kính R = 2 7 3
C. Tập hợp các điểm M là một mặt cầu có bán kính R = 7 2
D. Tập hợp các điểm M là một mặt cầu có bán kính R = 2 7 9
Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
![]()
![]()
![]()
![]()
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
![]()
![]()
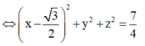
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2
Đúng 0
Bình luận (0)




