a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
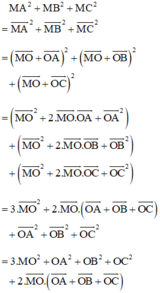
Lại có:
+ O là trọng tâm tam giác nên 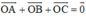
+ Bán kính đường tròn ngoại tiếp tam giác:
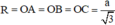
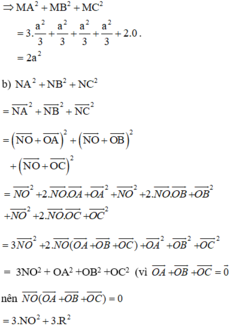
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.


