Cho A (3,4). Tìm hai điểm B,C trên trục Ox sao cho tam giác ABC đều
XO
Những câu hỏi liên quan
Trong không gian tọa độ Oxyz cho các điểm: A(1; -3; -1); và B(-2; 1; 3)
a) Chứng tỏ rằng hai điểm A và B cách đều trục Ox.
b) Tìm điểm C nằm trên Oz sao cho tam giác ABC vuông tại C.
c) Viết phương trình hình chiếu của đường thẳng AB trên mp(Oyz).
d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và có tâm nằm trên mp(Oyz).
a) \(Ox:\left\{{}\begin{matrix}x=t\\y=0\\z=0\end{matrix}\right.\).
Lấy điểm \(M\left(1;0;0\right)\in Ox\).
\(d\left(A,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\).
\(d\left(B,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\)
Do đó hai điểm \(A,B\) cách đều trục \(Ox\).
b) Điểm \(C\in Oz\) nên tọa độ điểm \(C\) có dạng \(\left(0;0;c\right)\).
Tam giác \(ABC\) vuông tại \(C\) nên \(CA\perp CB\)
suy ra \(\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow1.\left(-2\right)-3.1-\left(1+c\right).\left(3-c\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}c=-2\\c=4\end{matrix}\right.\).
c) Mặt phẳng \(\left(Oyz\right)\): \(x=0\).
Hình chiếu của \(A,B\) trên \(\left(Oyz\right)\) lần lượt là \(A'\left(0;-3;-1\right)\), \(B'\left(0;1;3\right)\).
Phương trình hình chiếu của đường thẳng \(AB\) trên \(\left(Oyz\right)\) là phương trình của đường thẳng \(A'B'\).
d) Gọi tọa độ tâm thỏa mãn yêu cầu bài toán là \(I\left(0;a;b\right)\).
Có \(IO=IA=IB\) suy ra
\(a^2+b^2=1^2+\left(a+3\right)^2+\left(b+1\right)^2=2^2+\left(a-1\right)^2+\left(b-3\right)^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-47}{16}\\b=\dfrac{53}{16}\end{matrix}\right.\).
Đúng 3
Bình luận (0)
Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
A. D( 5;0)
B. D( 7; 0)
C. D( 7,5 ;0)
D. tất cả sai
Chọn C.
Điểm D nằm trên trục Ox nên D( x; 0)
![]()
Mà: DA = DB ⇔DA2 = DB2
⇔ (2 – x)2 + 42 = (1 – x)2 + 22
⇔ 4 – 4x + x2 + 16 = 1 – 2x + x2 + 4
⇔ -2x = -15 ⇔x = 15/2. Suy ra: 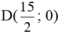
Đúng 0
Bình luận (0)
Cho đường tròn (C): x² + y² - 2x - 2y - m 0a) Tìm m để (C) cắt trục Oy tại hai điểm phân biệt A, B sao cho tam giác IAB là tam giác vuôngb) Tìm m để (C) cắt trục Ox tại hai điểm phân biệt A, B sao cho tam giác LAB là tam giác đềuc) Tìm m để (C) cắt đường thắng d: x - y + m 0 tại hai điểm phân biệt A, B sao cho tam giác IAB là tam giác cân có cạnh đáy bằng dfrac{2}{3}
Đọc tiếp
Cho đường tròn (C): x² + y² - 2x - 2y - m = 0
a) Tìm m để (C) cắt trục Oy tại hai điểm phân biệt A, B sao cho tam giác IAB là tam giác vuông
b) Tìm m để (C) cắt trục Ox tại hai điểm phân biệt A, B sao cho tam giác LAB là tam giác đều
c) Tìm m để (C) cắt đường thắng d: x - y + m = 0 tại hai điểm phân biệt A, B sao cho tam giác IAB là tam giác cân có cạnh đáy bằng \(\dfrac{2}{3}\)
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
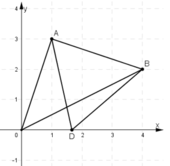
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
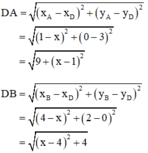
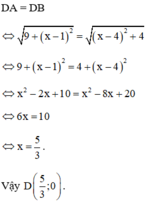
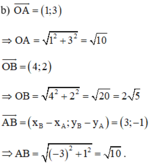
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
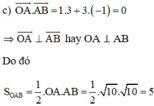
Đúng 0
Bình luận (0)
Cho ∠xOy = 90◦. a) Dựng tia Oz nằm giữa hai tia Ox, Oy sao cho ∠xOz = 30◦. b) Trên tia Ox,Oz lần lượt lấy các điểm A,B sao cho OA = OB (A,B ̸= O). Dựng về phía bên trong tam giác OAB tam giác đều ABC. Đường thẳng AC cắt Oy tại D. Chứng minh rằng C là trung điểm của AD. c) Chứng minh rằng đường trung trực của các đoạn thẳng CO,CB và tia Oy đồng quy. Giúp nình vơi!!
Trên mặt phẳng tọa độ Oxy cho hai điểm \(A\left(1;3\right);B\left(4;2\right)\)
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB
b) Tính chu vi tam giác OAB
c) Tính diện tích tam giác OAB
Cho góc xOy = 120o, tia phân giác là Oz. Trên tia Ox, Oy, Oz lấy 3 điểm A, B, C sao cho tam giác ABC đều. Chứng tỏ OA + OB = OC. Tìm bài toán ngược lại.
Xem thêm câu trả lời
Trong hệ trục tọa độ Oxyz, cho điểm H(2;1;1). Gọi các điểm A,B,C lần lượt ở trên các trục tọa độ Ox,Oy,Oz sao cho H là trực tâm của tam giác ABC. Khi đó hoành độ điểm A là:
A. -3
B. -5
C. 3
D. 5
Cho hai điểm \(A\left( {1;3} \right),B\left( {4;2} \right)\)
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA=DB
b) Tính chu vi tam giác OAB
c) Chứng minh rằng OA vuông góc AB và từ đó tính diện tích tam giác OAB
a) Gọi tọa độ điểm D là \((x;0)\)
Ta có: \(\overrightarrow {DB} = \left( {4 - x;2} \right) \Rightarrow DB = \left| {\overrightarrow {DB} } \right| = \sqrt {{{\left( {4 - x} \right)}^2} + {2^2}} \)
\(\begin{array}{l}DA = DB \Leftrightarrow \sqrt {{{\left( {1 - x} \right)}^2} + {3^2}} = \sqrt {{{\left( {4 - x} \right)}^2} + {2^2}} \\ \Rightarrow {\left( {1 - x} \right)^2} + {3^2} = {\left( {4 - x} \right)^2} + {2^2}\\ \Rightarrow x^2 -2x+10 = x^2 -8x+ 20\\ \Rightarrow 6x = 10\\ \Rightarrow x = \frac{5}{3}\end{array}\)
Thay \(x = \frac{5}{3}\) ta thấy thảo mãn phương trình
Vậy khi \(D\left( {\frac{5}{3};0} \right)\) thì DA=DB
b) Ta có: \(\overrightarrow {OA} = \left( {1;3} \right) \Rightarrow OA = \left| {\overrightarrow {OA} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} \)
\(\overrightarrow {OB} = \left( {4;2} \right) \Rightarrow OB = \left| {\overrightarrow {OB} } \right| = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 \)
\(\overrightarrow {AB} = \left( {3; - 1} \right) \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \)
Chu vi tam giác OAB là
\({C_{OAB}} = OA + OB + AB = \sqrt {10} + 2\sqrt 5 + \sqrt {10} = 2\sqrt {10} + 2\sqrt 5 \)
c) \(\overrightarrow {OA} .\overrightarrow {AB} = 1.3 + 3.( - 1) = 0 \Rightarrow OA \bot AB\)
Tam giác OAB vuông tại A nên diện tích của tam giác là
\({S_{OAB}} = \frac{1}{2}OA.AB = \frac{1}{2}\sqrt {10} .\sqrt {10} = 5\)
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác ABC có A (-1;1) , B( 5;3) , C thuộc Oy, G thuộc Ox. Tìm tọa độ điểm C. tính S∆ABC
Câu 2:Cho A(-1;2) ,d :x-2y+3=0. tìm trên đường thẳng đi hai điểm B,C sao cho ∆ ABC vuông tại C và AC=3BC
Xem chi tiết
Câu 1 đề thiếu, điểm C thỏa mãn điều gì nữa? (ví dụ G là trọng tâm tam giác?)
Câu 2:
Do B, C đều thuộc d nên tọa độ có dạng: \(B\left(2b-3;b\right);C\left(2c-3;c\right)\) với \(b\ne c\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2c-2;c-2\right)\\\overrightarrow{BC}=\left(2c-2b;c-b\right)\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{BC}=0\\AC=3BC\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(2c-2\right)\left(2c-2b\right)+\left(c-2\right)\left(c-b\right)=0\\\left(2c-2\right)^2+\left(c-2\right)^2=9\left(2c-2b\right)^2+9\left(c-b\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4c-4+c-2=0\\\left(2c-2\right)^2+\left(c-2\right)^2=45\left(c-b\right)^2\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 1
Bình luận (0)




