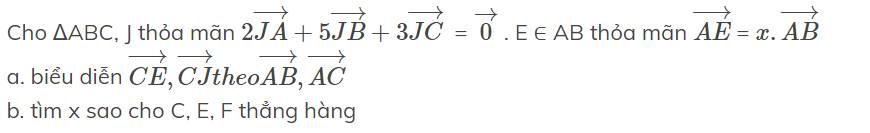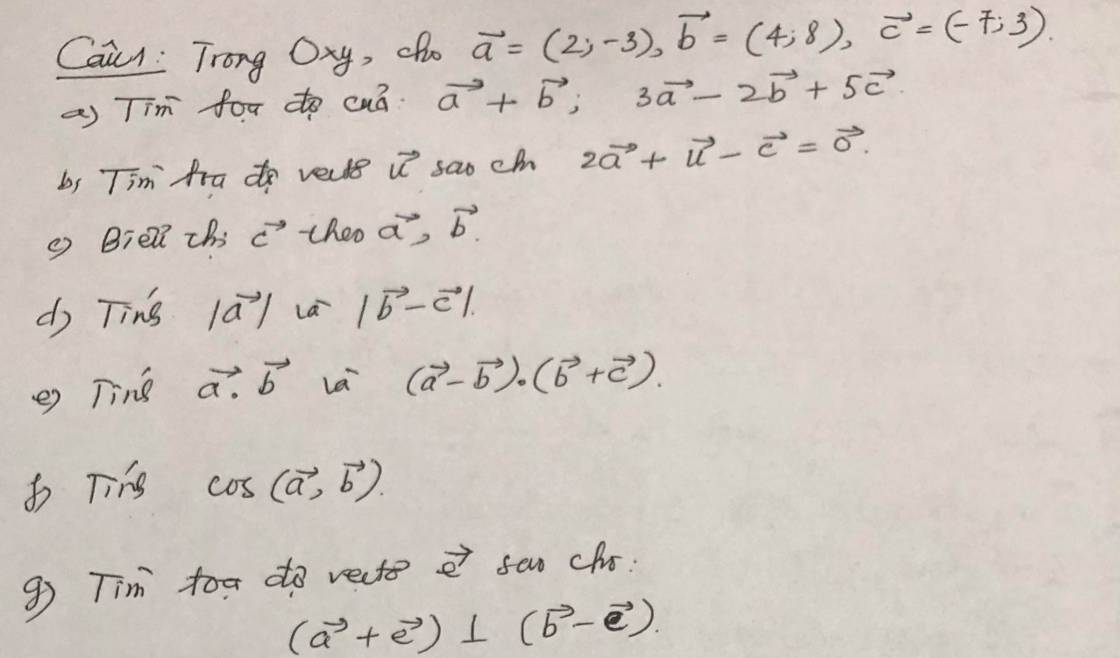cho hình vuông abcd ,gọi e là trung điểm ab,f là điểm sao cho af =1/3ad,m là điểm trên đường thẳng bc sao cho mc=k.bc .tìm giá trị k để 2 đường thẳng ef và fm vuông góc với nhau
Ôn tập chương II
ΔABC, trên AB, AC lấy M, N sao cho \(\dfrac{AM}{MB}\text{=}\dfrac{2}{5}\) ; \(\dfrac{BN}{NC}\text{=}\dfrac{1}{3}\) ; I là giao điểm AN, CM. Tính tỉ số \(\dfrac{AI}{AN};\dfrac{CI}{IM}\)
Cho ΔABC, J thỏa mãn 2overrightarrow{JA}+5overrightarrow{JB}+3overrightarrow{JC} overrightarrow{0} . E ∈ AB thỏa mãn overrightarrow{AE} x.overrightarrow{AB}a. biểu diễn overrightarrow{CE},overrightarrow{CJ}theooverrightarrow{AB},overrightarrow{AC}b. tìm x sao cho C, E, F thẳng hàng
Đọc tiếp
Cho ΔABC, J thỏa mãn \(2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}\) = \(\overrightarrow{0}\) . E ∈ AB thỏa mãn \(\overrightarrow{AE}\) = \(x.\overrightarrow{AB}\)
a. biểu diễn \(\overrightarrow{CE},\overrightarrow{CJ}theo\overrightarrow{AB},\overrightarrow{AC}\)
b. tìm x sao cho C, E, F thẳng hàng
cho △ABC. tìm tập hợp điểm M thỏa mãn \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) bằng \(\dfrac{3}{2}\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Gọi G là trọng tâm của tam giác ABC, I là trung điểm BC.
Dễ dàng chứng minh \(\left\{{}\begin{matrix}\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\\\dfrac{3}{2}\left|\overrightarrow{MB}+\overrightarrow{MC}\right|=\dfrac{3}{2}\left|2\overrightarrow{MI}\right|=3MI\end{matrix}\right.\)
Kết hợp điều kiện đề bài, ta có \(MG=MI\). Do đó M nằm trên đường trung trực của GI (cố định).
Vậy tập hợp điểm M thoả điều kiện đề bài là trung trực của đoạn GI.
Đúng 0
Bình luận (0)
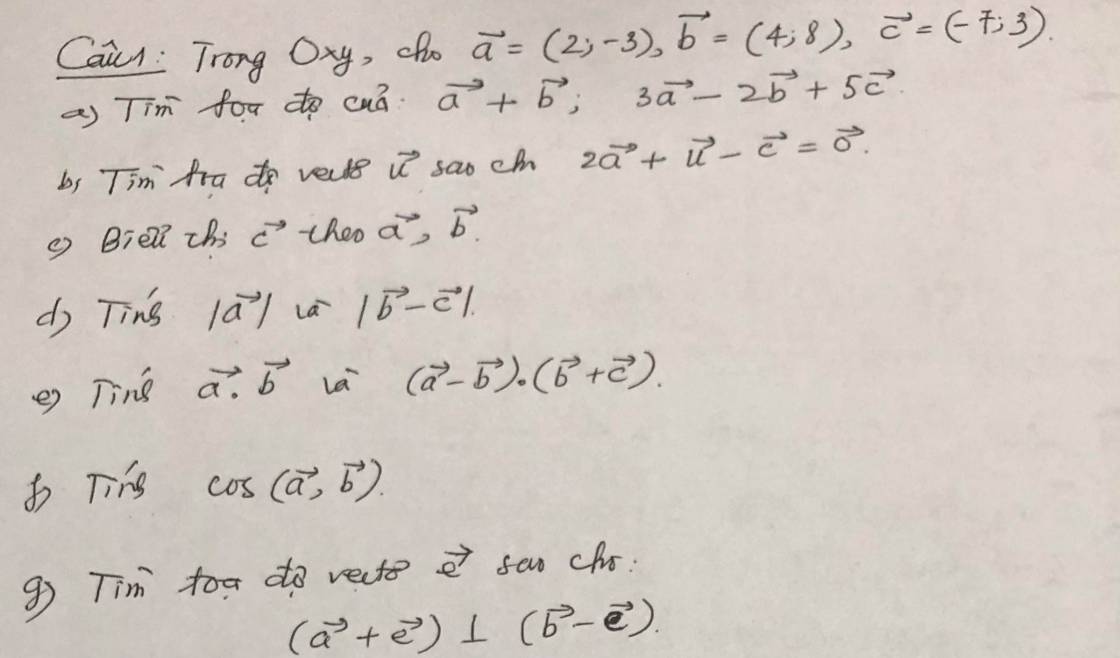 giúp mình với 🆘
giúp mình với 🆘
a: \(\overrightarrow{a}=\left(2;-3\right);\overrightarrow{b}=\left(4;8\right);\overrightarrow{c}=\left(-7;3\right)\)
Tọa độ của \(\overrightarrow{a}+\overrightarrow{b}\) là:
\(\left\{{}\begin{matrix}x=2+4=6\\y=-3+8=5\end{matrix}\right.\)
Tọa độ của \(3\overrightarrow{a}-2\overrightarrow{b}+5\overrightarrow{c}\) là:
\(\left\{{}\begin{matrix}x=3\cdot2-2\cdot4+5\left(-7\right)=-37\\y=3\cdot\left(-3\right)-2\cdot8+5\cdot3=-10\end{matrix}\right.\)
b: \(\overrightarrow{2a}+\overrightarrow{u}-\overrightarrow{c}=\overrightarrow{0}\)
=>\(\overrightarrow{u}=-2\overrightarrow{a}+\overrightarrow{c}\)
Tọa độ của vecto u là:
\(\left\{{}\begin{matrix}x=-2\cdot2+\left(-7\right)=-11\\y=-2\cdot\left(-3\right)+3=6+3=9\end{matrix}\right.\)
c: Đặt \(\overrightarrow{c}=x\cdot\overrightarrow{a}+y\cdot\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}-7=2x+4y\\3=-3x+8y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+8y=-14\\-3x+8y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=-17\\-3x+8y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{17}{7}\\8y=3x+3=\dfrac{-51}{7}+3=-\dfrac{30}{7}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{17}{7}\\y=-\dfrac{30}{7\cdot8}=-\dfrac{30}{56}=-\dfrac{15}{28}\end{matrix}\right.\)
Vậy: \(\overrightarrow{c}=-\dfrac{17}{7}\cdot\overrightarrow{a}+\dfrac{-15}{28}\cdot\overrightarrow{b}\)
d: \(\left|\overrightarrow{a}\right|=\sqrt{2^2+\left(-3\right)^2}=\sqrt{13}\)
\(\overrightarrow{b}-\overrightarrow{c}=\left(11;5\right)\)
=>\(\left|\overrightarrow{b}-\overrightarrow{c}\right|=\sqrt{11^2+5^2}=\sqrt{146}\)
e: \(\overrightarrow{a}\cdot\overrightarrow{b}=2\cdot4+\left(-3\right)\cdot8=-24+8=-16\)
\(\overrightarrow{a}-\overrightarrow{b}=\left(-2;-11\right);\overrightarrow{b}+\overrightarrow{c}=\left(-3;11\right)\)
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{b}+\overrightarrow{c}\right)=\left(-2\right)\cdot\left(-3\right)+\left(-11\right)\cdot11=-121+6=-115\)
f: \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{-16}{\sqrt{2^2+\left(-3\right)^2}\cdot\sqrt{4^2+8^2}}\)
\(=\dfrac{-16}{\sqrt{13}\cdot4\sqrt{5}}=-\dfrac{4}{\sqrt{65}}\)
Đúng 1
Bình luận (1)
Cho hình bình hành abcd trên cạnh AB lấy 3 điểm phân biệt trên cạnh CD lấy 5 điểm phân biệt Hỏi có bao nhiêu tam giác mà các đỉnh của nó được lấy từ đỉnh của hình bình hành và 8 điểm nói trên
Một hộp đựng 40 cây viết được đánh số từ 1 đến 40. Chọn ngẫu nhiên 5 cây. Xác suất để chọn được 5 cây mang tổng chẵn là
Có 20 cây số lẻ (1;3;5...;39) và 20 cây số chẵn (2;4;...;40)
Để tổng 5 cây là chẵn \(\Rightarrow\) số cây lẻ phải chẵn
\(\Rightarrow\) Các trường hợp thỏa mãn gồm: 0 lẻ 5 chẵn, 2 lẻ 3 chẵn, 4 lẻ 1 chẵn
\(\Rightarrow C_{20}^5+C_{20}^2.C_{20}^3+C_{20}^4.C_{20}^1\) cách chọn thỏa mãn
Đúng 1
Bình luận (0)
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Để cho dễ tính toán, ta coi như việc chọn 2 số là theo thứ tự
Không gian mẫu: \(A_{90}^2\)
Chọn số thứ nhất: \(C_{90}^1=90\) cách
Hàng đơn vị số thứ 2 có 1 cách chọn (giống hàng đơn vị số thứ nhất), hàng chục số thứ 2 có 8 cách chọn (khác hàng chục số thứ hai và 0)
\(\Rightarrow90.1.8\) cách chọn 2 số thỏa mãn yêu cầu
Xác suất: \(P=\dfrac{90.1.8}{A_{90}^2}\)
Đúng 2
Bình luận (0)
Bài này thực ra rất dễ chọn, vì 2 nữ ở Lý hết rồi. Do đó chọn 2 nữ có 1 cách
Giờ chọn 2 nam (có nữ + lý nên giờ có Toán là được): có 2 trường hợp: 2 nam cùng toán, hoặc 1 nam toán 1 nam lý.
Vậy là xong
Đúng 2
Bình luận (0)