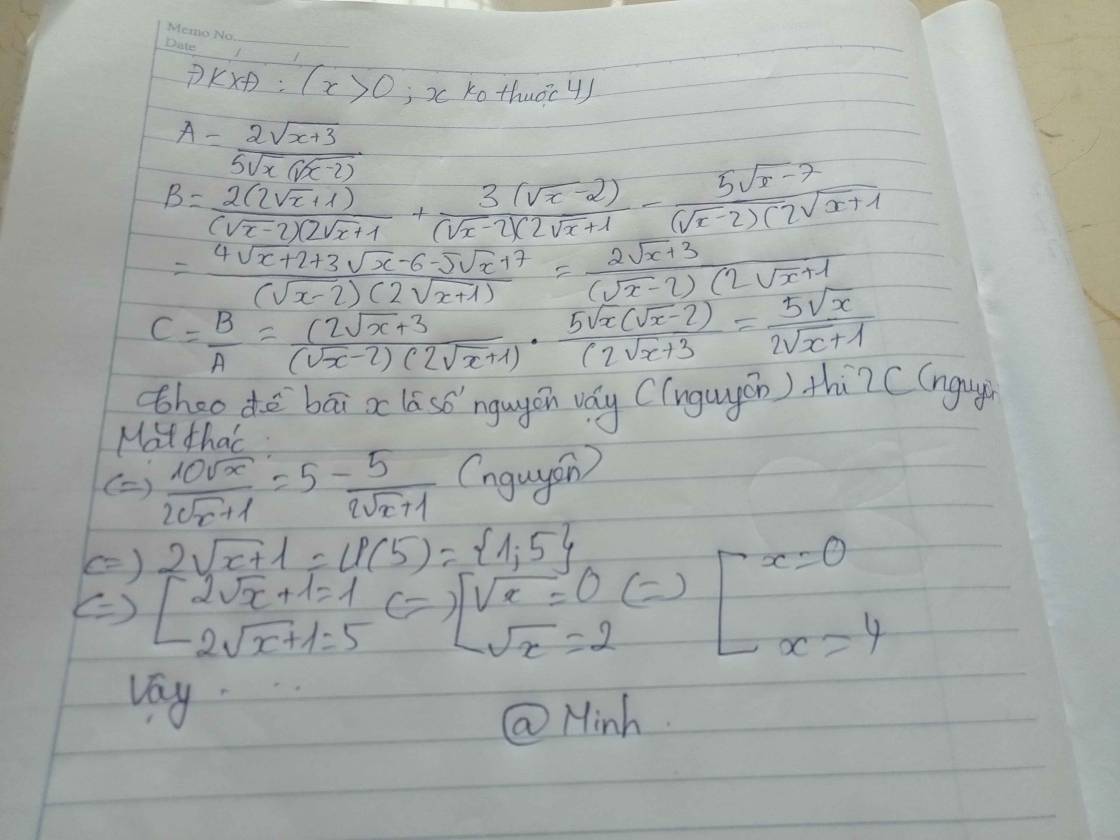Tìm số nguyên a sao cho: \(\dfrac{-5}{2}< \dfrac{a}{5}< \dfrac{1}{4}\)
KJ
Những câu hỏi liên quan
Tìm số nguyên a sao cho : \(-\dfrac{5}{12}< \dfrac{a}{5}< \dfrac{1}{4}\)
\(\text{#040911}\)
Vì \(-\dfrac{5}{12}< 0\)
\(\Rightarrow-\dfrac{5}{12}< \dfrac{a}{5}\text{ }\forall\text{ }a\)
\(\dfrac{a}{5}< \dfrac{1}{4}\)
\(\Rightarrow a=1\)
Vậy, để thỏa mãn \(-\dfrac{5}{12}< \dfrac{a}{5}< \dfrac{1}{4}\) thì \(a=1.\)
Đúng 1
Bình luận (0)
Ta có - 5/12 <a/5<1/4
ta có 2/5>1/4 mà 1/5 <1/4
nên a = 1
Đúng 0
Bình luận (0)
a) Cho phân số \(\dfrac{13}{42}\). Hãy tìm một số tự nhiên n sao cho khi cộng tử số với n và giữ nguyên mẫu số thì được phân số mới có giá trị bằng \(\dfrac{5}{6}\).
b) Tính nhanh
\(\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{6}+\dfrac{4}{8}+\dfrac{5}{10}+\dfrac{6}{12}+\dfrac{7}{14}+\dfrac{8}{16}+\dfrac{9}{18}+\dfrac{10}{20}\)
Bài 9: Tìm x biết1) dfrac{9}{x}dfrac{-35}{105} 2) dfrac{12}{5}dfrac{32}{x} 3) dfrac{x}{2}dfrac{32}{x} 4) dfrac{x-2}{4}dfrac{x-1}{5}Bài 10: Cho biểu thức Adfrac{3}{n+2}a) Số nguyên n phài thỏa mãn điều kiện gì để A là phân số? b) Tìm phân số A khi n 0? n 2? n -7?
Đọc tiếp
Bài 9: Tìm \(x\) biết
1) \(\dfrac{9}{x}=\dfrac{-35}{105}\) 2) \(\dfrac{12}{5}=\dfrac{32}{x}\) 3) \(\dfrac{x}{2}=\dfrac{32}{x}\) 4) \(\dfrac{x-2}{4}=\dfrac{x-1}{5}\)
Bài 10: Cho biểu thức \(A=\dfrac{3}{n+2}\)
a) Số nguyên n phài thỏa mãn điều kiện gì để A là phân số? b) Tìm phân số A khi n = 0? n = 2? n = -7?
Bài 10:
a: Để A là phân số thì n+2<>0
hay n<>-2
b: Khi n=0 thì A=3/2
Khi n=2 thì A=3/(2+2)=3/4
Khi n=-7 thì A=3/(-7+2)=-3/5
Đúng 1
Bình luận (0)
Bài 9:
1)9/x = -35/105 2) 12/5 = 32/x 3)x/2 = 32/x x = 9. (-35)/105 x.12/5 = x.32/x 2x.x/2 = 2x.32/x
x = -3 x.12/5=32 xx = 2.32
x= 32:12/5 x^2 = 2.32
x = 40/3 x^2 = 64
x = 8
4) x-2/4 = x-1/5
5(x-2) = 4(x-1)
5x - 10 = 4x - 4
5x - 4x = 10 - 4
x = 6
Bài 10:Cho biểu thức
Đúng 1
Bình luận (0)
Tìm số nguyên x, biết:
a) -4dfrac{3}{5}. 2dfrac{4}{3} x -2dfrac{3}{5} : 1dfrac{6}{15}
b) -4dfrac{1}{3}.(dfrac{1}{2}-dfrac{1}{6}) x - dfrac{2}{3}.(dfrac{1}{3} - dfrac{1}{2} - dfrac{3}{4})
Đọc tiếp
Tìm số nguyên x, biết:
a) \(-4\dfrac{3}{5}\). \(2\dfrac{4}{3}\) < x < \(-2\dfrac{3}{5}\) : \(1\dfrac{6}{15}\)
b) \(-4\dfrac{1}{3}\).(\(\dfrac{1}{2}\)-\(\dfrac{1}{6}\)) < x < - \(\dfrac{2}{3}\).(\(\dfrac{1}{3}\) - \(\dfrac{1}{2}\) - \(\dfrac{3}{4}\))
a) Ta có \(-4\dfrac{3}{5}\cdot2\dfrac{4}{3}=-\dfrac{23}{5}\cdot\dfrac{10}{3}=-\dfrac{46}{3}\) và \(-2\dfrac{3}{5}\div1\dfrac{6}{15}=-\dfrac{13}{5}\div\dfrac{7}{5}=-\dfrac{13}{7}\)
Do đó \(-\dfrac{46}{3}< x< -\dfrac{13}{7}\)
Lại có \(-\dfrac{46}{3}\le-15\) và \(-\dfrac{13}{7}\ge-2\)
Suy ra \(-15\le x\le-2\), x ϵ Z
b) Ta có \(-4\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{6}\right)=-\dfrac{13}{3}\cdot\dfrac{1}{3}=-\dfrac{13}{9}\) và \(-\dfrac{2}{3}\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{3}{4}\right)=-\dfrac{2}{3}\cdot\dfrac{-11}{12}=\dfrac{11}{18}\)
Do đó \(-\dfrac{13}{9}< x< \dfrac{11}{18}\)
Lại có \(-\dfrac{13}{9}\le-1\) và \(\dfrac{11}{18}\ge0\)
Suy ra \(-1\le x\le0\), x ϵ Z
Đúng 1
Bình luận (0)
b, -4\(\dfrac{1}{3}\).(\(\dfrac{1}{2}\) - \(\dfrac{1}{6}\)) < \(x\) < - \(\dfrac{2}{3}\).(\(\dfrac{1}{3}\) - \(\dfrac{1}{2}\) - \(\dfrac{3}{4}\))
- \(\dfrac{13}{3}\).\(\dfrac{1}{3}\) < \(x\) < - \(\dfrac{2}{3}\).(-\(\dfrac{11}{12}\))
- \(\dfrac{13}{9}\) < \(x\) < \(\dfrac{11}{18}\)
\(x\) \(\in\) { -1; 0; 1}
Đúng 0
Bình luận (0)
a, -4\(\dfrac{3}{5}\).2\(\dfrac{4}{3}\) < \(x\) < -2\(\dfrac{3}{5}\): 1\(\dfrac{6}{15}\)
- \(\dfrac{23}{5}\).\(\dfrac{10}{3}\) < \(x\) < - \(\dfrac{13}{5}\): \(\dfrac{21}{15}\)
- \(\dfrac{46}{3}\) < \(x\) < - \(\dfrac{13}{7}\)
\(x\) \(\in\) {-15; -14;-13;..; -2}
Đúng 1
Bình luận (0)
Cho A=\(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}vaB=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\)
a)tính giá trị của bt A khi x=2
b)rút gọn bt B
c) tìm x sao cho bt P=-A.B nhận giá trị là số nguyên
Cho hai biểu thức \(A=\dfrac{2\sqrt{x}+3}{5x-10\sqrt{x}}\) và \(B=\dfrac{2}{\sqrt{x}-2}+\dfrac{3}{2\sqrt{x}+1}-\dfrac{5\sqrt{x}-7}{2x-3\sqrt{x}-2}\) với x>0, x≠4. Tìm x sao cho \(\dfrac{B}{A}\)nhận giá trị là một số nguyên.
Tìm n ϵ Z sao cho n là số nguyên
\(\dfrac{2n-1}{n-1};\dfrac{3n+5}{n+1};\dfrac{4n-2}{n+3};\dfrac{6n-4}{3n+4};\dfrac{n+3}{2n-1};\dfrac{6n-4}{3n-2};\dfrac{2n+3}{3n-1};\dfrac{4n+3}{3n+2}\)
tìm các số nguyên a,b sao cho:\(\dfrac{-3}{8}< \dfrac{a}{10}< \dfrac{-3}{5}\)
Giả sử tồn tại số nguyên a thỏa mãn đề bài khi đó:
- \(\dfrac{3}{8}\) < - \(\dfrac{3}{5}\) ⇒ \(\dfrac{3}{8}\) > \(\dfrac{3}{5}\) (khi nhân cả hai vế của bất đẳng thức với một số âm thì dấu của bất đẳng thức đổi chiều)
⇒ 8 < 5 (vô lý) hay điều giả sử là sai
Vậy không tồn tại số nguyên nào thỏa mãn đề bài
Kết luận: a \(\in\) \(\varnothing\)
Đúng 0
Bình luận (0)
Bài 11: Cho biểu thức A = \(\dfrac{9-3x}{x^2+4x-5}-\dfrac{x+5}{1-x}-\dfrac{x+1}{x+5}\) (với x ≠ -5; x ≠ 1)
a) Rút gọn A b) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
c) Tìm x sao cho A<0 d) Tìm x sao cho |A| = 3
\(a,A=\dfrac{9-3x+x^2+10x+25-x^2+1}{\left(x-1\right)\left(x+5\right)}\\ A=\dfrac{7x+35}{\left(x-1\right)\left(x+5\right)}=\dfrac{7\left(x+5\right)}{\left(x-1\right)\left(x+5\right)}=\dfrac{7}{x-1}\\ b,A\in Z\\ \Leftrightarrow x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-6;0;2;8\right\}\left(tm\right)\\ b,A< 0\Leftrightarrow x-1< 0\left(7>0\right)\\ \Leftrightarrow x< 1;x\ne-5\\ c,\left|A\right|=3\Leftrightarrow\dfrac{7}{\left|x-1\right|}=3\Leftrightarrow\left|x-1\right|=\dfrac{7}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}+1=\dfrac{10}{3}\left(tm\right)\\x=-\dfrac{7}{3}+1=-\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
1.Tìm các số tự nhiên a,b khác 0 sao cho : dfrac{a}{5}-dfrac{z}{b}dfrac{2}{15}.2.Tìm số tự nhiên n, để các biểu thức là số tự nhiên.a)Adfrac{4}{n-1}+dfrac{6}{n-1}-dfrac{3}{n-1}.b)Bdfrac{2n+9}{n+2}-dfrac{3n}{n+2}+dfrac{5n+1}{n+2}.giúp mình với mai mình nộp rồi
Đọc tiếp
1.Tìm các số tự nhiên a,b khác 0 sao cho :
\(\dfrac{a}{5}-\dfrac{z}{b}=\dfrac{2}{15}\).
2.Tìm số tự nhiên n, để các biểu thức là số tự nhiên.
a)A=\(\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\).
b)B=\(\dfrac{2n+9}{n+2}-\dfrac{3n}{n+2}+\dfrac{5n+1}{n+2}\).
giúp mình với mai mình nộp rồi![]()
Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
Đúng 4
Bình luận (0)
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0
Đúng 0
Bình luận (0)