\(\begin{array}{l}1.\,\,\,\,\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right] \Leftrightarrow 2\cos a.\cos b = \cos \left( {a + b} \right) + \cos \left( {a - b} \right)\\ \Leftrightarrow 2\cos \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \cos u + \cos v\\2.\,\,\,\,\sin a.\sin b =  - \frac{1}{2}.\left[ {\cos \left( {a + b} \right) - \cos \left( {a - b} \right)} \right] \Leftrightarrow  - 2.\sin a.\sin b = \cos \left( {a + b} \right) - \cos \left( {a - b} \right)\\ \Leftrightarrow  - 2.\sin \frac{{u + v}}{2}.\sin \frac{{u - v}}{2} = \cos u - \cos v\\3.\,\,\,\,\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right] \Leftrightarrow 2\sin a.\cos b = \sin \left( {a + b} \right) + \sin \left( {a - b} \right)\\ \Leftrightarrow 2\sin \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \sin u + \sin v\\4.\,\,\,\,\sin \left( {a + b} \right) - \sin \left( {a - b} \right) = \sin a.\cos b + \cos a.\sin b - \sin a.\cos b + \cos a.\sin b = 2\cos a.\sin b\\ \Leftrightarrow \sin u - \sin v = 2.\cos \frac{{u + v}}{2}.\sin \frac{{u - v}}{2}\end{array}\)

\(A=2sin\dfrac{a+b}{2}cos\dfrac{a-b}{2}+2sin\dfrac{a+b}{2}cos\dfrac{a+b}{2}\)

\(=2sin\dfrac{a+b}{2}\left(cos\dfrac{a+b}{2}+cos\dfrac{a-b}{2}\right)\)

\(=2sin\dfrac{a+b}{2}.2cos\dfrac{a}{2}cos\dfrac{b}{2}\)

\(=4sin\dfrac{a+b}{2}cos\dfrac{a}{2}cos\dfrac{b}{2}\)

`1) cos x + sin 2x - cos 3x`

`= -2sin 2x . (-sin x) + sin 2x`

`= sin 2x ( 2 sin x + 1 )`

Cấu 2 hình như sai đề bạn ạ phải là `sin 3x + sin x` chứ :v

Lời giải:
$A=\sin ^2a-\sin ^2b=(\sin a-\sin b)(\sin a+\sin b)$

$B$ không biến đổi được. Bạn coi lại đề.

Khi hai viên bi sắt va chạm, lực do viên bi 1 tác dụng lên viên bi 2 làm biến dạng viên bi 2. (Nếu 2 viên bi va chạm mạnh thì chúng sẽ bị sứt mẻ, vỡ gây biến dạng).

Chọn đáp án A.

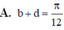
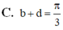
Chọn D

Bổ trợ kiến thức: Ở những dạng toán trên ta khó có thể biến đổi để xử lí trên máy tính cầm tay, có lẽ ở đây ra nên sử dụng hình thức tự luận để giải quyết một bài toán trắc nghiệm không quá khó khăn. Học sinh cần ghi nhớ một số công thức được sử dụng trong bài toán trên: 

Câu a tiếp tục ko dịch được đề :)

b.

\(\Leftrightarrow1+cos3x=sin^2\frac{x}{2}+cos^2\frac{x}{2}+2sin\frac{x}{2}.cos\frac{x}{2}\)

\(\Leftrightarrow1+cos3x=1+sinx\)

\(\Leftrightarrow cos3x=sinx\)

\(\Leftrightarrow cos3x=cos\left(\frac{\pi}{2}-x\right)\)

\(\Leftrightarrow...\)

c.

\(\Leftrightarrow cos8x+cos2x+sinx=cos8x\)

\(\Leftrightarrow cos2x+sinx=0\)

\(\Leftrightarrow cos2x=-sinx\)

\(\Leftrightarrow cos2x=cos\left(\frac{\pi}{2}+x\right)\)

\(\Leftrightarrow...\)

d.

\(sin\left(3x-\frac{\pi}{6}\right)=-\left(1-2sin^2\frac{x}{2}\right)\)

\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=-cosx\)

\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin\left(x-\frac{\pi}{2}\right)\)

\(\Leftrightarrow...\)