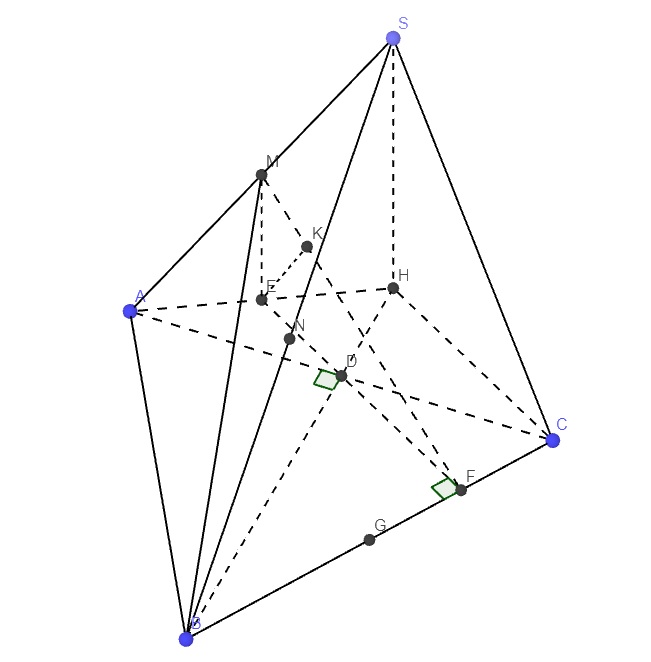
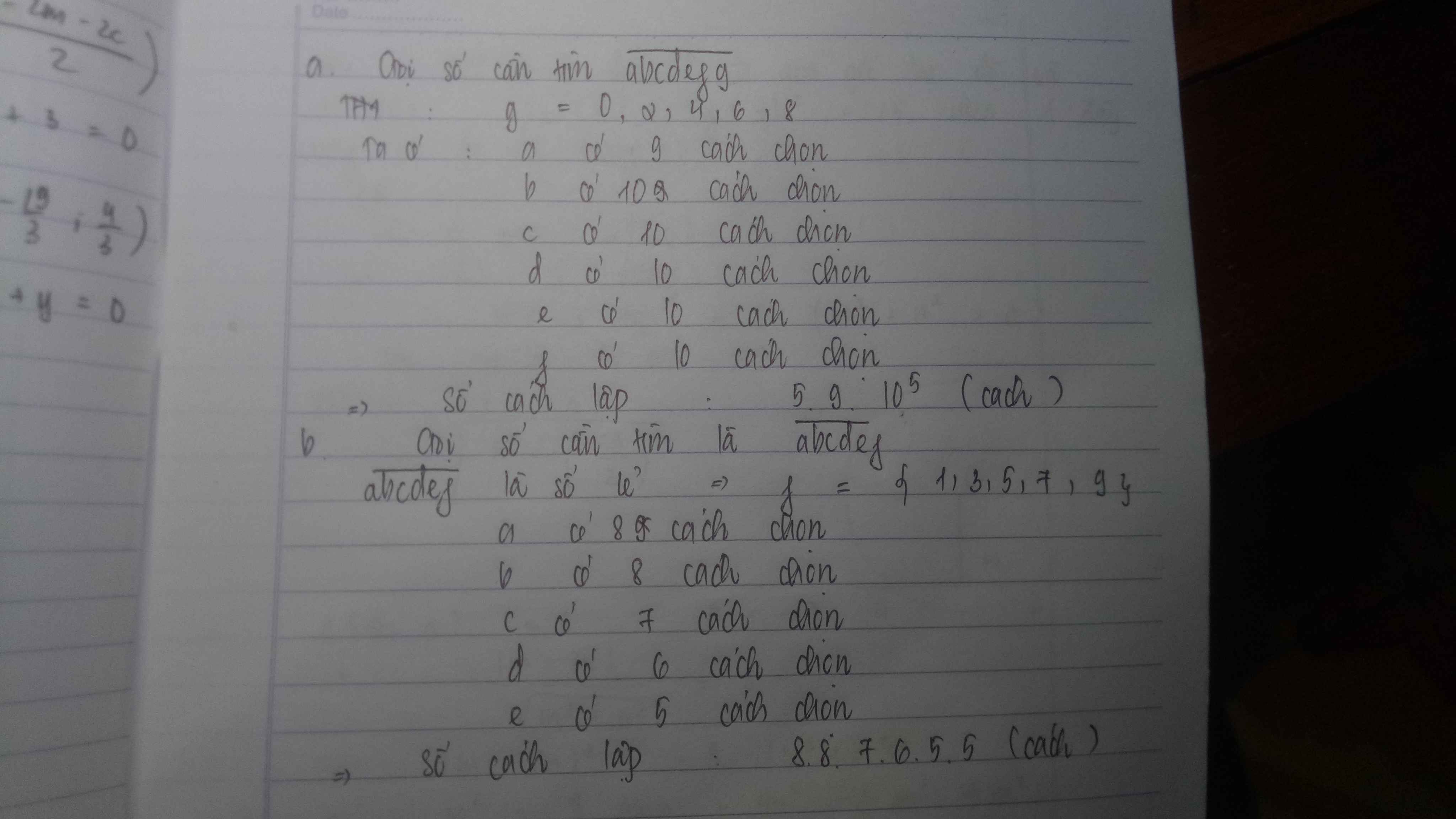giúp e bài này ạ e cảm ơn ac ạ
NH
Những câu hỏi liên quan
mn giúp e bài này với ạ, e cảm ơn ạ
mn giúp e bài này với ạ, e cảm ơn ạ
chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2
Đúng 1
Bình luận (0)
Giúp e 3 bài này gấp với ạ. Phiền mn giúp e với ạ. E cảm ơn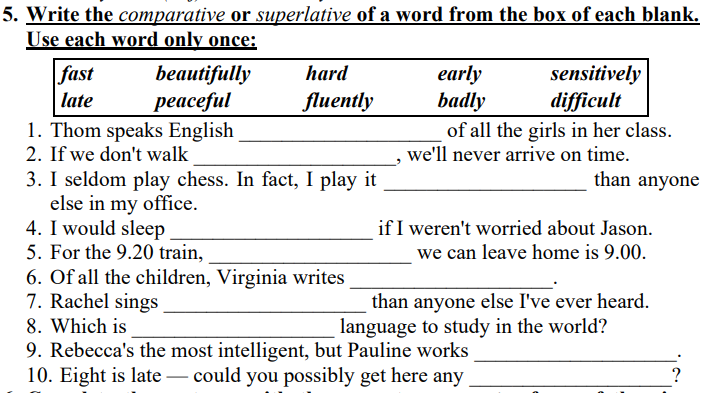
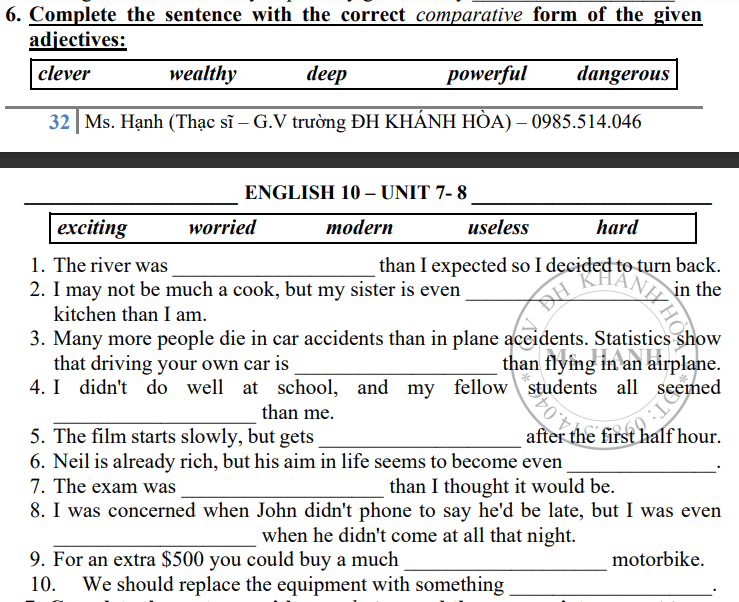

bạn đăng tách ra tầm 10 câu mỗi lần đăng nha, chứ dài ntnay ngại làm lắm~
Đúng 0
Bình luận (1)
Mng giúp e bài này với ạ, e cảm ơn nhiều ạ
giúp e bài này với ạ. e cảm ơn nhiều ạ :3
a: \(P=\dfrac{8}{x\left(x+4\right)}+\dfrac{5x}{x\left(x+4\right)}-\dfrac{2x+8}{x\left(x+4\right)}=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
b: Thay x=1/2 vào P, ta được:
P=3:9/2=3x2/9=6/9=2/3
Đúng 0
Bình luận (0)
Với khác 0 ; x khác 4
\(P=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3x}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
Thay x = 1/2 vào P ta được \(\dfrac{3}{\dfrac{1}{2}+4}=\dfrac{3}{\dfrac{9}{2}}=3:\dfrac{9}{2}=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
mn giúp e bài này với ạ, e cảm ơn ạ :')
a, \(n_{CaCO_3}=\dfrac{41,2}{100}=0,412\left(mol\right)\)
PTHH: CaO + H2O → Ca(OH)2
Mol: 0,412 0,412
PTHH: Ca(OH)2 + CO2 → CaCO3 + H2O
Mol: 0,412 0,412 0,412
\(m_{CaO}=0,412.56=23,072\left(g\right)\)
b, \(V_{CO_2}=0,412.22,4=9,2288\left(l\right)\)
Đúng 2
Bình luận (0)
\(m_{Na_2CO_3}=100.16,96\%=16,96\left(g\right)\Rightarrow n_{Na_2CO_3}=\dfrac{16,96}{106}=0,16\left(mol\right)\)
\(m_{BaCl_2}=200.10,4\%=20,8\left(g\right)\Rightarrow n_{BaCl_2}=\dfrac{20,8}{208}=0,1\left(mol\right)\)
PTHH: Na2CO3 + BaCl2 → BaCO3 + 2NaCl
Mol: 0,1 0,1 0,2
Ta có: \(\dfrac{0,16}{1}>\dfrac{0,1}{1}\) ⇒ Na2CO3 dư, BaCl2 hết
mdd sau pứ = 100 + 200 = 300 (g)
\(C\%_{ddNaCl}=\dfrac{0,1.58,5.100\%}{300}=1,95\%\)
\(C\%_{ddNa_2CO_3}=\dfrac{\left(0,16-0,1\right).106.100\%}{300}=2,12\%\)
Đúng 2
Bình luận (0)
 Mn giúp e bài này vs ạ , e cảm ơn nhìu ạ!
Mn giúp e bài này vs ạ , e cảm ơn nhìu ạ!
Thầy cô hướng dẫn giúp e bài này ạ, e cảm ơn ạ
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
Đúng 1
Bình luận (0)
Giải giúp e bài hình này với ạ
E đang cần gấp ạ , e cảm ơn

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
Đúng 0
Bình luận (0)
Giúp e bài này với ạ,e đang cần gấp.E cảm ơn trước ạ!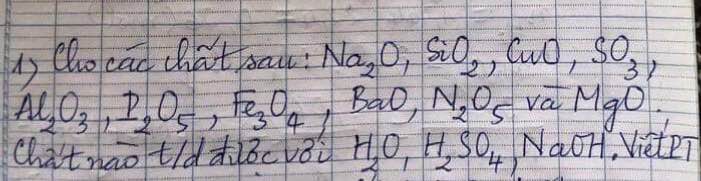
Tác dụng với \(H_2O:\)\(Na_2O,SO_3,P_2O_5,BaO,N_2O_5,SiO_2\)
Tác dụng với \(H_2SO_4:Na_2O,CuO,Al_2O_3,Fe_3O_4,BaO,MgO\)
Tác dụng với NaOH: \(SiO_2,P_2O_5,N_2O_5,SO_3\)
Đúng 2
Bình luận (0)