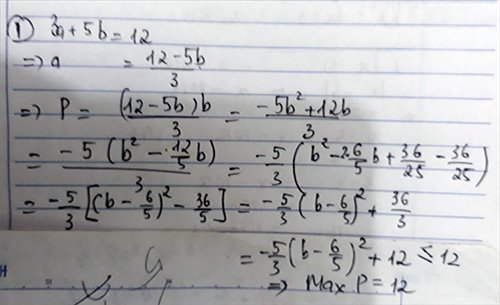tìm min,max của M = 2016+ xy biết \(2x^2+\frac{1}{x^2}+\frac{4}{y^2}=4\)
PP
Những câu hỏi liên quan
1. Cho Afrac{3}{2+sqrt{2x-x^2}+3}a. Tìm x để A có nghĩab. Tìm Min(A), Max(A)2/ Tìm Min, Max của: Afrac{1}{2+sqrt{x-x^2}}3/ Tìm Min(B) biết: Bsqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}4/ Tìm Min, Max của:Cfrac{4x+3}{x^2+1}5/ Tìm Max của: Asqrt{x-1}+sqrt{y-2}biết x+y46/ Tìm Max(B) biết: Bfrac{ysqrt{x-1}+xsqrt{y-2}}{xy}7/ Tìm Max(C) biết: Cx+sqrt{2-x}
Đọc tiếp
1. Cho A=\(\frac{3}{2+\sqrt{2x-x^2}+3}\)
a. Tìm x để A có nghĩa
b. Tìm Min(A), Max(A)
2/ Tìm Min, Max của: \(A=\frac{1}{2+\sqrt{x-x^2}}\)
3/ Tìm Min(B) biết: \(B=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
4/ Tìm Min, Max của:\(C=\frac{4x+3}{x^2+1}\)
5/ Tìm Max của: \(A=\sqrt{x-1}+\sqrt{y-2}\)biết \(x+y=4\)
6/ Tìm Max(B) biết: \(B=\frac{y\sqrt{x-1}+x\sqrt{y-2}}{xy}\)
7/ Tìm Max(C) biết: \(C=x+\sqrt{2-x}\)
tích mình với
ai tích mình
mình tích lại
thanks
Đúng 0
Bình luận (0)
Cho x,y là hai số thực thỏa mãn \(2x^2+\frac{y^2}{4}:\frac{1}{x^2}=3\) . Tìm Max,Min của B = 2020 + xy
1.tìm max A(frac{x}{x+2020})^2 với x0
2. tìm min C frac{left(4x+1right)left(4+xright)}{x} với x dương
3.cho 3a+5b12. tìmmin Bab
4.tìm min x^2-x+4+frac{1}{x^2-x}
5. cho x,y là 2 số thỏa mãn 2x^2+frac{1}{x^2}+frac{y}{4}4.tìm min max của xy
6. cho a,b0 và a+b1. tìm min Mleft(1+frac{1}{a}right)^2left(1+frac{1}{b}right)^2
Đọc tiếp
1.tìm max A=(\(\frac{x}{x+2020}\))\(^2\) với x>0
2. tìm min C= \(\frac{\left(4x+1\right)\left(4+x\right)}{x}\) với x dương
3.cho 3a+5b=12. tìmmin B=ab
4.tìm min \(x^2-x+4+\frac{1}{x^2-x}\)
5. cho x,y là 2 số thỏa mãn \(2x^2+\frac{1}{x^2}+\frac{y}{4}=4\).tìm min max của xy
6. cho a,b>0 và a+b=1. tìm min M=\(\left(1+\frac{1}{a}\right)^2\left(1+\frac{1}{b}\right)^2\)
Cho x,y thỏa mãn: 2x2 + y2 + \(\frac{1}{x^2}\)= 4. Tìm Max - Min của p = xy. giúp mình vs mn ơi
\(x^2+x^2+y^2+\frac{1}{x^2}\ge4\sqrt[4]{x^2y^2}\)
\(\Rightarrow4\sqrt[4]{x^2y^2}\le4\Rightarrow\sqrt[4]{x^2y^2}\le1\Rightarrow x^2y^2\le1\)
\(\Rightarrow-1\le xy\le1\)
\(P_{max}=1\) khi \(\left(x;y\right)=\left(1;1\right);\left(-1;-1\right)\)
\(P_{min}=-1\) khi \(\left(x;y\right)=\left(1;-1\right);\left(-1;1\right)\)
Đúng 0
Bình luận (0)
1.Tìm min của
A=-x2+3x+4 với 1=<x=<2
2.Cho x+y+z=3
Tìm min của P=-xy+3xyz+4xz
3.Cho m,n,p thỏa mãn 2m2+2n2+4p2+3mn+mp+2np=\(\frac{3}{2}\)
Tìm min, max A=m+n+p+2016
Nhờ mn nha mh cảm ơn
Cho \(x,y\ne0\) thỏa mãn \(2x^2+\dfrac{1}{x^2}+\dfrac{y^4}{4}=4\) .
Tìm MIN, MAX của : P= \(xy+2021\)
Em kiểm tra đề là \(\dfrac{y^2}{4}\) hay \(\dfrac{y^4}{4}\)
Nếu đề đúng là \(\dfrac{y^4}{4}\) thì có thể coi như là không giải được
Đúng 1
Bình luận (1)
\(2x^2+\dfrac{1}{x^2}+\dfrac{y^2}{4}=4\Leftrightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(x^2-xy+\dfrac{y^2}{4}\right)+xy=2\)
\(\Leftrightarrow2=\left(x-\dfrac{1}{x}\right)^2+\left(x-\dfrac{y}{2}\right)^2+xy\ge xy\)
\(\Rightarrow P_{max}=2023\) khi \(\left\{{}\begin{matrix}x-\dfrac{1}{x}=0\\x-\dfrac{y}{2}=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-1;-2\right);\left(1;2\right)\)
\(2x^2+\dfrac{1}{x^2}+\dfrac{y^2}{4}=4\Leftrightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(x^2+xy+\dfrac{y^2}{4}\right)-xy=2\)
\(\Rightarrow2=\left(x-\dfrac{1}{x}\right)^2+\left(x+\dfrac{y}{2}\right)^2-xy\ge-xy\)
\(\Rightarrow xy\ge-2\Rightarrow P\ge2019\)
\(P_{min}=2019\) khi \(\left\{{}\begin{matrix}x-\dfrac{1}{x}=0\\x+\dfrac{y}{2}=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-1;2\right);\left(1;-2\right)\)
Đúng 2
Bình luận (1)
1, Cho x 0, y 0, x + y le1
Tìm MinA frac{1}{x^2+y^2}+frac{2}{xy}+4xy
2, Tìm Min và max của P frac{x^2+1}{x^2-x+1}
3, Cho (x + y)2 + 7(x + y) +y2 + 10 0
Tìm min, Max của P x + y + 1
4, Cho x 0, y 0 và x + y le1
CMR : frac{1}{x^2+xy}+frac{1}{y^2+xy}ge4
Đọc tiếp
1, Cho x > 0, y > 0, x + y \(\le\)1
Tìm MinA = \(\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy\)
2, Tìm Min và max của P = \(\frac{x^2+1}{x^2-x+1}\)
3, Cho (x + y)2 + 7(x + y) +y2 + 10 = 0
Tìm min, Max của P = x + y + 1
4, Cho x > 0, y > 0 và x + y \(\le\)1
CMR : \(\frac{1}{x^2+xy}+\frac{1}{y^2+xy}\ge4\)
1.
Đầu tiên ta cm: \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\forall a,b>0\)
Ta có:
\(\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}\ge\frac{2\sqrt{ab}}{ab}=\frac{2}{\sqrt{ab}}\ge\frac{2}{\frac{a+b}{2}}=\frac{4}{a+b}\) (cô si)
Dấu "=" khi a = b.
Áp dụng:
\(\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy\) \(=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(\frac{1}{4xy}+4xy\right)+\frac{5}{4xy}\)
\(\ge\frac{4}{\left(x+y\right)^2}+2\sqrt{\frac{1}{4xy}\cdot4xy}+\frac{5}{\left(x+y\right)^2}\)
\(=4+2+5=11\)
Vậy MinA = 11 khi \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
\(P=\frac{x^2+1}{x^2-x+1}\Leftrightarrow x^2+1=P\left(x^2-x+1\right)\)
\(\Leftrightarrow x^2+1-Px^2+Px-P=0\)(*)
\(\Leftrightarrow\left(1-P\right)x^2+Px+\left(1-P\right)=0\)
\(\Delta=P^2-4\left(1-P\right)^2\)
\(=P^2-4\left(1-2P+P^2\right)=-3P^2+8P-4\)
Để P có GTNN và GTLN thì phương trình (*) có nghiệm
\(\Leftrightarrow\Delta\ge0\Leftrightarrow-3P^2+8P-4\ge0\)
\(\Leftrightarrow-3P^2+2P+6P-4\ge0\)
\(\Leftrightarrow-P\left(3P-2\right)+2\left(3P-2\right)\ge0\)
\(\Leftrightarrow\left(3P-2\right)\left(2-P\right)\ge0\)
\(\Leftrightarrow\frac{2}{3}\le P\le2\)
Vậy \(min_P=\frac{2}{3}\Leftrightarrow x=-1\); \(max_P=2\Leftrightarrow x=1\)
Đúng 0
Bình luận (0)
\(\left(x+y\right)^2+7\left(x+y\right)+y^2+10=0\)
\(\Leftrightarrow\left(x+y\right)^2+2\cdot\left(x+y\right)\cdot\frac{7}{2}+\frac{49}{4}-\frac{9}{4}=-y^2\)
\(\Leftrightarrow\left(x+y+\frac{7}{2}\right)^2-\frac{9}{4}=-y^2\)
\(\Leftrightarrow\left(x+y+2\right)\left(x+y+5\right)=-y^2\le0\)
Vì \(x+y+2< x+y+5\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+2\le0\\x+y+5\ge0\end{matrix}\right.\Leftrightarrow-5\le x+y\le-2\)
\(\Leftrightarrow-4\le x+y+1\le-1\)
Vậy: \(Min=-4\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.;Max=-1\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Cho a, b là các hằng số dương. Tìm min Ax+y biết x0, y0; frac{a}{x}+frac{b}{y}12.Tìm ain Z, a#0 sao cho max và min của Afrac{12xleft(x-aright)}{x^2+36}cũng là số nguyên3. Cho Afrac{x^2+px+q}{x^2+1} . Tìm p, q để max A9 và min A-14. Tìm min Pfrac{1}{1+xy}+frac{1}{1+yz}+frac{1}{1+xz} với x,y,z0 ; x^2+y^2+z^2le35. Tìm min P3x+2y+frac{6}{x}+frac{8}{y} với x+yge6 6. Tìm min, max Pxsqrt{5-x}+left(3-xright)sqrt{2+x} với 0le xle37.Tìm min Aleft(x+frac{1}{x}right)^2+left(y+frac{1}{y}right)^2 với x0,...
Đọc tiếp
1. Cho a, b là các hằng số dương. Tìm min A=x+y biết x>0, y>0; \(\frac{a}{x}+\frac{b}{y}=1\)
2.Tìm \(a\in Z\), a#0 sao cho max và min của \(A=\frac{12x\left(x-a\right)}{x^2+36}\)cũng là số nguyên
3. Cho \(A=\frac{x^2+px+q}{x^2+1}\) . Tìm p, q để max A=9 và min A=-1
4. Tìm min \(P=\frac{1}{1+xy}+\frac{1}{1+yz}+\frac{1}{1+xz}\) với x,y,z>0 ; \(x^2+y^2+z^2\le3\)
5. Tìm min \(P=3x+2y+\frac{6}{x}+\frac{8}{y}\) với \(x+y\ge6\)
6. Tìm min, max \(P=x\sqrt{5-x}+\left(3-x\right)\sqrt{2+x}\) với \(0\le x\le3\)
7.Tìm min \(A=\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2\) với x>0, y>0; x+y=1
8.Tìm min, max \(P=x\left(x^2+y\right)+y\left(y^2+x\right)\) với x+y=2003
9. Tìm min, max P = x--y+2004 biết \(\frac{x^2}{9}+\frac{y^2}{16}=36\)
10. Tìm mã A=|x-y| biết \(x^2+4y^2=1\)
Giải dùm:
a, Tìm Min , Max:
4x-16\(\sqrt{x}\)+4y-22\(\sqrt{y}\)-4\(\sqrt{xy}\)+36
b,Tìm Max: \(\frac{6\sqrt{x}+3}{2x+4}\)
c,Tìm Min: \(\frac{2}{1-x}+\frac{1}{x}\left(0< x< 1\right)\)
Ukm
It's very hard
l can't do it
Sorry!
Đúng 0
Bình luận (0)