Cho lời giải chi tiết ạ
KH
Những câu hỏi liên quan
Giúp mk lm bài hai ạ
Cho mk xin lời lời giải chi tiết ạ
Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
DO đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
Đúng 1
Bình luận (1)
Giải giúp mình với lời giải chi tiết ạ^^
Giải nhanh nhanh em tick cho ạ 
Giúp mình với ạ cho mk xin lời giải chi tiết ạ
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
b: Xét ΔOEF có
OM là đường cao
OM là đường phân giác
Do đó: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của FE
hay FM=EM
Đúng 3
Bình luận (0)
Cho mình lời giải chi tiết với ạ
1: \(A=6x^3y^5\)
\(B=4x^4y^6\cdot\left(-x\right)^6y^3=-4x^{10}y^9\)
2: Hệ số của A là 6
Phần biến của A là x mũ 3; y mũ 5
Bậc của A là 8
Hệ số của B là -4
Phần biến của B là x^10; y^9
Bậc là 19
Đúng 0
Bình luận (0)
Kèm lời giải chi tiết cho e ạ :
Đọc tiếp
Kèm lời giải chi tiết cho e ạ <:
=>5/13>5/p>5/5q>5/16
=>13<p<5q<16
=>p=14; 5q=15
=>p=14; q=3
Đúng 1
Bình luận (0)
Cho em xin lời giải chi tiết ạ

cho em lời giải chi tiết với ạ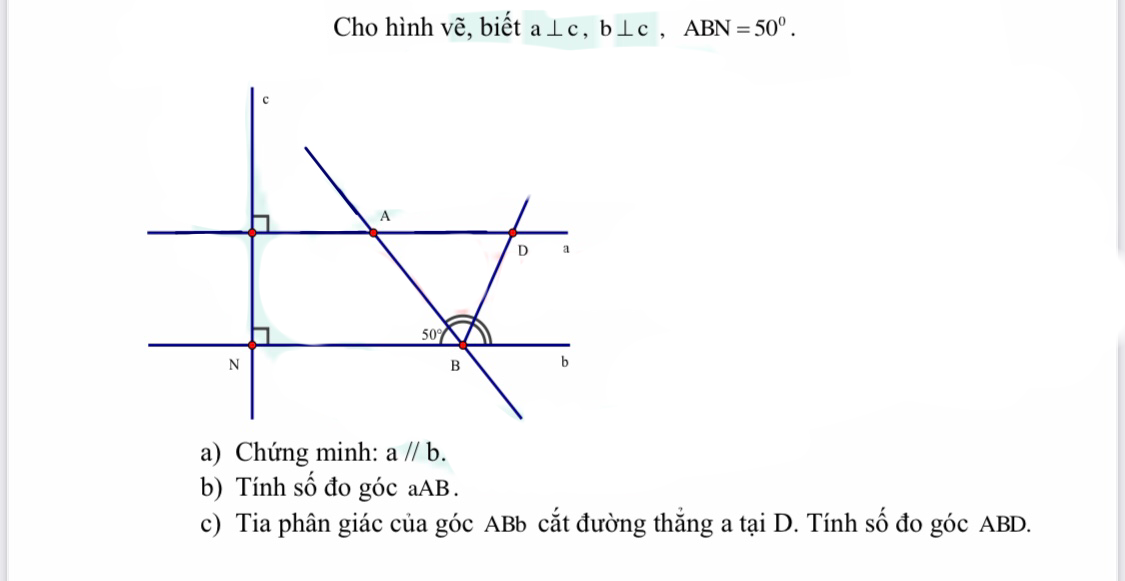
Mình cần lời giải chi tiết ạ
Làm nhanh mình tick cho ạ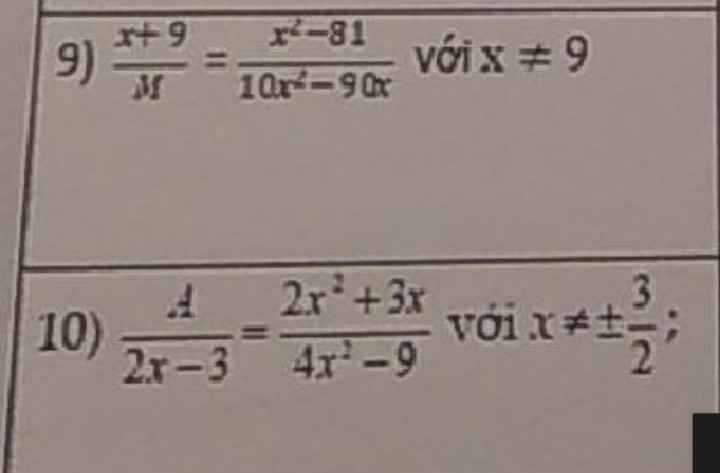
\(9,\dfrac{x^2-81}{10x^2-90x}=\dfrac{\left(x-9\right)\left(x+9\right)}{10x\left(x-9\right)}=\dfrac{x+9}{10x}\Rightarrow M=10x\\ 10,\dfrac{2x^2+3x}{4x^2-9}=\dfrac{x\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}=\dfrac{x}{2x-3}\Rightarrow A=x\)
Đúng 1
Bình luận (0)
\(9,M=\dfrac{\left(x+9\right)\left(10x^2-90x\right)}{x^2-81}=\dfrac{10x\left(x+9\right)\left(x-9\right)}{\left(x-9\right)\left(x+9\right)}=10x\\ 10,A=\dfrac{\left(2x-3\right)\left(2x^2+3x\right)}{4x^2-9}=\dfrac{x\left(2x+3\right)\left(2x-3\right)}{\left(2x-3\right)\left(2x+3\right)}=x\)
Đúng 1
Bình luận (0)
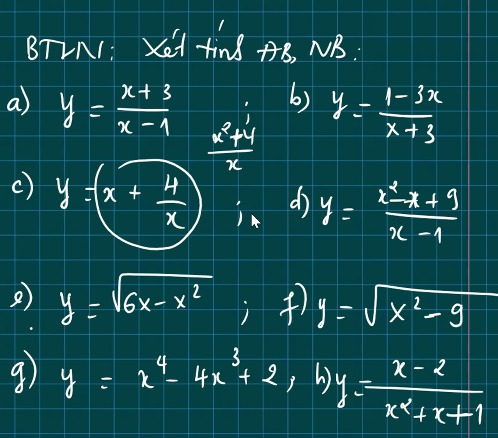 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ
f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
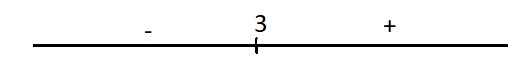
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
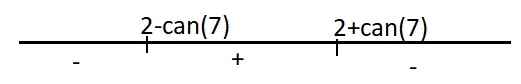
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)
Đúng 0
Bình luận (0)
Cho mik xin lời giải chi tiết vs ạ




