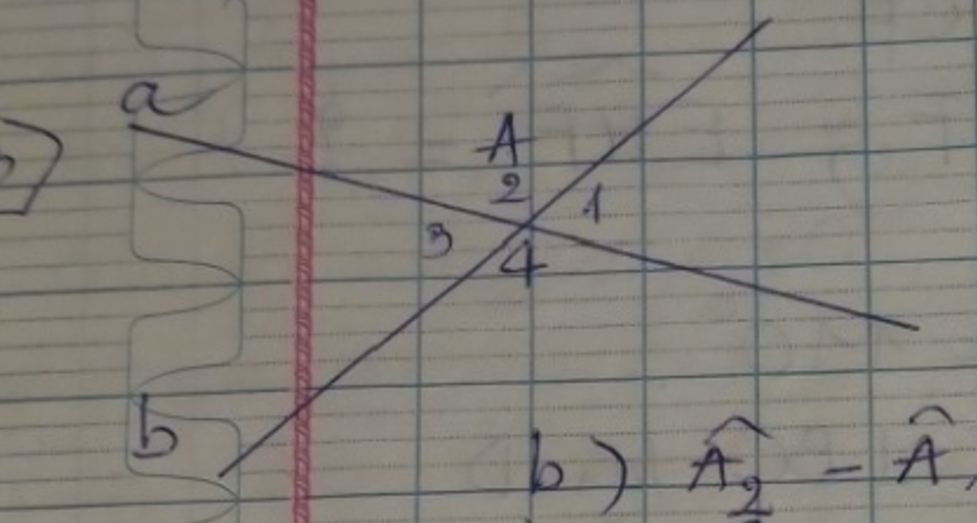
Tính số đo các góc \(Â_1;Â_2;Â_3;Â_4\), biết \(Â_2-Â_1=30^O\)
Hình minh họa...
a) Góc ngoài của một tam giác cân có số đo bằng 1300 . Tính số đo các góc tam giác đó. b) Góc ngoài của một tam giác cân có số đo bằng 800 . Tính số đo các góc tam giác đó.
cho góc xoy có số đo là 35 vẽ góc yox kề bù với góc tính số đo góc yox vẽ góc xoy đối đỉnh với góc tính số đo các góc còn lại trên hình
cho tia Ot nằm giữa hai tia ox và oy biết số đo góc xot = 30 độ số đo góc xoy = 80 độ
a tính số đo góc toy
b gọi om, on lần lượt là tia phân giác của các góc xot và toy. tính số đo các góc mot và not
c tính số đo góc mon
Vẽ góc BOC có só đo = 60 độ và vẽ tia OA nằm giữa hai tia OB , OC .
a ) Biết số đo góc AOC = 2 lần số đo góc BOA . Tính số đo các góc BOA , góc AOC
b ) Vẽ tia OD là tia đối của tia OB . Tính số đo các góc COD , góc AOD
Tính số đo các góc của tam giác ABC. Biết rằng: tỉ số giữa số đo góc A và số đo góc B là 3 : 4, tỉ số giữa số đo góc B và số đo góc C là 3 : 5.
Các bạn giải chi tiết theo cách lớp 7 giúp mình nhé!!! Cảm ơn các bạn rất nhiều!!!
Gọi x;y;z lần lượt là các góc của tam giác ABC:
X/3=Y/4=Z/5 và x+y+z=180
Áp dụng tính chất của dãy tỉ số bằng nhau:
X/3=Y/4=Z/5=X+Y+Z/3+4+5=180/12=15
*X/3=15 SUY RA X=3 X 15 = 45
*Y/4=15 SUY RA Y= 4 X 15=60
*Z/5 =15 SUY RA Z=5 X 15 =75
Vây x=45
y=60
z=75
Gọi số đo các góc lần lượt là a , b , c
Theo đề bài ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5};a+b+c=180\)( Định lý tổng 3 góc của tam giác bạn nhé )
Áp dụng tính chất dãy tỉ số bằng nhau ta có ;
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\Rightarrow\)\(a=15.3=45\)
\(b=15.4=60\)
\(c=15.5=75\)
Vậy số đo các góc của tam giác lần lượt là 45 độ ; 60 độ ; 75 độ
Nếu bạn không tin thì có thể lấy ba số : 45 + 60 + 75 = 180 độ ( đúng bạn nhé )
3) Cho hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo bằng 450.
a) Tính số đo góc NAQ.
b) Tính số đo góc MAQ .
c Viết tên các cặp góc đối đỉnh.
d) Viết tên các cặp góc kề bù nhau.
a) Ta có:
∠MAP= ∠NAQ (hai góc đối đỉnh)
⇒ ∠NAQ = 45o
⇒ ∠NAQ = 45o
b) Ta có:
∠MAP + ∠MAQ = 180o ( hai góc kề bù )
⇒ 45o + ∠MAQ = 180o
⇒ ∠MAQ = 180o − 45o = 135o
c) Các cặp góc đối đỉnh là:
∠MAP, ∠NAQ
∠NAP, ∠MAQ
d) Các cặp góc bù nhau là:
∠MAP, ∠NAP
∠MAP, ∠MAQ
∠NAQ, ∠NAP
∠NAQ, ∠MAQ
Tính số đo các góc của 1 tam giác , biết số đo thứ nhất bằng 2/3 số góc đo thứ 2 và số góc đo thứ 2 bằng 3/5 số góc đo thứ 3
Tính số đo các góc của tam giác, biết rằng số đo góc thứ thất bằng 2/3 số đo góc thứ hai và bằng 1/2 số đo góc thứ ba.
Cả 2 cạnh thứ nhất và thứ 2 là
\(\frac{2}{3}+\frac{1}{2}=\frac{7}{6}\)
Hình tam giác có 3 cạnh nên ta tính như sau
\(\Rightarrow\) Số đo của hình tam giác đó là \(3\times\frac{7}{6}=3,5\)
\(\Leftrightarrow\) Vậy cạnh của hình tam giác đó là \(3,5\)
Tôi giải mà chẳng biết đúng hay sai. Tôi mới sắp lên lớp 6
Tỉ số giữa góc T1 và T2 là: 2/3
Tỉ số giữa góc T1 và T3 là: 1/2
Quy đồng:
1/2 = 2/4
Vậy tỉ số giữa góc T1; T2; T3 là: 2/3/4
Tổng số phần bằng nhau là:
2 + 3 + 4 = 9 (phần)
Lại có tổng số đo các góc trong một tam giác là: 180o
=> \(\widehat{A}=180:9.2=40^o\)| \(\widehat{B}=180:9.3=60^o\)| \(\widehat{C}=180:9.4=80^o\)
Đ/S: 40o; 60o; 80o
Chúc bạn học tốt !!!
P/s: Em năm nay mới lên lớp 6 có gì sai thông cảm
Tính số đo các góc của một tam giác, biết số đo góc thứ nhất bằng 2/3 số đo góc thứ hai và số đo góc thứ hai bằng 3/5 số đo góc thứ ba
Gọi số đo góc thứ 1 là 2a thì số đo góc thứ 2 là \(3a\) và số đo góc thứ 3 là \(5a\)
Ta có: \(2a+3a+5a=180^0\Rightarrow10a=180^0\Rightarrow a=18^0\)
Số đó góc thứ 1 là: \(2.18^0=36^0\)
Số đó góc thứ 2 là: \(3.18^0=54^0\)
Số đo góc thứ 3 là: \(5.18^0=90^0\)
tam giác ABC có số đo các góc là góc A , góc B , góc C lần lượt tỉ lệ với 1;2;3 . Tính số đo các góc của ΔABC.
Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=\frac{180^0}{6}=30^0\) (định lý tổng 3 góc trong tam giác)
\(\Rightarrow \widehat{A}=30^0; \widehat{B}=2.30^0=60^0; \widehat{C}=3.30^0=90^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180}{6}=30\)
Do đó: a=30; b=60; c=90