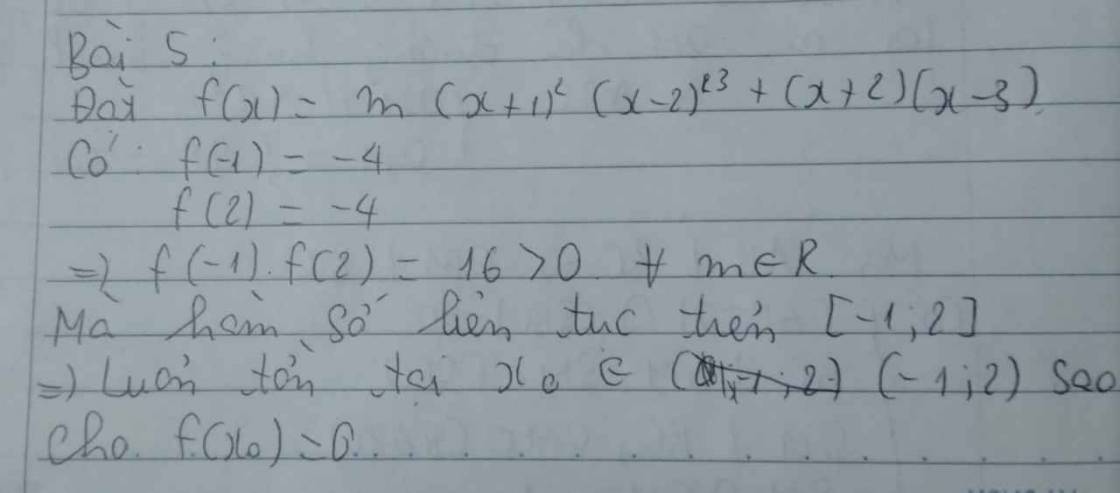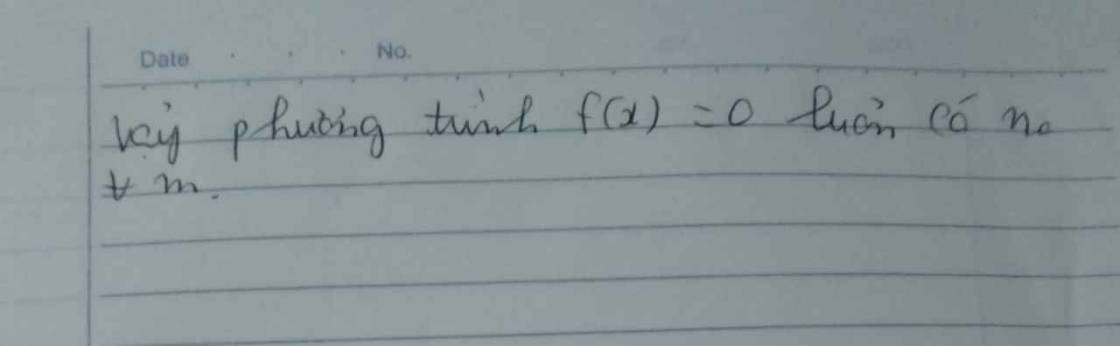Chứng minh rằng với mọi x > 1 ta luôn có: \(3\left(x^2-\frac{1}{x^2}\right)
NK
Những câu hỏi liên quan
Chứng minh rằng với mọi \(x,y\) ta luôn có
\(\left(x,y+1\right)\left(x^2y^2-xy+1\right)+\left(x^3-1\right)\left(1-y^3\right)=x^3+y^3\)
Nhanh lên ạ giúp mình zới :>
cả nhà giúp mk 2 bài này vs
1) giải pt \(x\left(x^2+9\right)\left(x+9\right)=22\left(x-1\right)^2\)
2) chứng minh rằng vs mọi x>1 ta luôn có \(3\left(x^2-\frac{1}{x^2}\right)< 2\left(x^3-\frac{1}{x^3}\right)\)
PT cho tđuong với: (x^2 +9). (x^2 + 9x) = 22 (x-1)^2
Đặt t = [x^2 + 9 + x^2 + 9x]/2 hay t= x^2 + (9x + 9)/2.
Khi đó: x^2 + 9 = t - 9(x-1)/2
x^2 + 9x = t + 9(x-1)/2
PT cho trở thành: [t - 9(x-1)/2]. [t + 9(x-1)/2] = 22(x-1)^2
<=> t^2 -(81/4)(x-1)^2 = 22(x-1)^2
<=> t^2 = (169/4)(x-1)^2
<=> t = 13/2. (x-1) hoặc t= -13/2. (x-1)
<=> 2t =13x -13 hoặc 2t =-13x + 13
hay 2x^2 + 9x+ 9 =13x -13 hoặc 2x^2 + 9x +9 = -13x +13
hay 2x^2 - 4x +22 =0 hoặc 2x^2 + 22x - 4 =0
PT bậc hai thứ nhất vô nghiệm, PT bậc hai thứ hai cho ta hai nghiệm là:
x= (-11 +căn(129))/2 , x= (-11 - căn(129))/2.
Đúng 0
Bình luận (0)
cách 2:đặt x-1=k
pt trở thành (k+1)(k2+2k+10)(k+10)=22k2
<=>(k2+2k+10)(k2+11k+10)=22k2
tự làm tiếp
Đúng 0
Bình luận (0)
cách 3:tui ko nhớ rõ nhưng nhân tung rồi nhóm lại là đc
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình sau luôn có nghiệm với mọi tham số $m$:
$m{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{3}}+\left( x+2 \right)\left( x-3 \right)=0$.
Xét hàm số f(x)=m(x+1)2(x−2)3+(x+2)(x−3)f(x)=m(x+1)2(x−2)3+(x+2)(x−3) xác định và liên tục trên RR
⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].
Ta có: {f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2{f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2.
+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0
⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.
+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0
⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).
Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.
Đúng 0
Bình luận (0)
Xét hàm số \(f\left(x\right)=m\left(x+1\right)^2\left(x-2\right)^3+\left(x+2\right)\left(x-3\right)\)
f(x)=m(x+1)2(x−2)3+(x+2)(x−3), \(D=ℝ\)
R⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].
Ta có: \(\left\{{}\begin{matrix}f\left(-2\right)=-64m\\f\left(3\right)=16m\end{matrix}\right.\)
\(\Rightarrow f\left(-2\right).f\left(3\right)=-1024m^2\)
+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0
⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.
+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0
⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).
Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi x ta luôn có :
\(\left(2x+1\right)\sqrt{x^2-x+1}>\left(2x-1\right)\sqrt{x^2+x+1}\)
Chứng minh rằng với \(x>1\)
ta luôn có: \(3\left(x^2-\frac{1}{x^2}\right)<2\left(x^3-\frac{1}{x^3}\right)\)
chứng minh công thức sau: Với mọi \(x\inℕ^∗\)ta luôn có : \(\frac{2}{x\left(x+2\right)}=\frac{1}{x}-\frac{1}{x+2}\)
Để mình đưa công thức tổng quát luôn khỏi mất công bạn đăng câu hỏi cho mệt =.=
Với mọi \(a,n\inℕ^∗\)
Cần chứng minh :
\(\frac{n}{a\left(a+n\right)}=\frac{1}{a}-\frac{1}{a+n}\)
Ta có :
\(\frac{1}{a}-\frac{1}{a+n}=\frac{a+n}{a\left(a+n\right)}-\frac{a}{a\left(a+n\right)}=\frac{a+n-a}{a\left(a+n\right)}=\frac{n}{a\left(a+n\right)}\) ( đpcm )
Vậy với mọi \(a,n\inℕ^∗\) thì \(\frac{n}{a\left(a+n\right)}=\frac{1}{a}-\frac{1}{a+n}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
Ta có :
\(\frac{1}{x}-\frac{1}{x+2}=\frac{x+2}{x\left(x+2\right)}-\frac{x}{x\left(x+2\right)}=\frac{x+2-x}{x\left(x+2\right)}=\frac{2}{x\left(x+2\right)}\) ( đpcm )
Vậy với mọi \(x\inℕ^∗\) ta luôn có \(\frac{2}{x\left(x+2\right)}=\frac{1}{x}-\frac{1}{x+2}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
Mình mới nghĩ ra một cách chứng minh khác nàk bạn tham khảo nhé :)
Ta có công thức tổng quát :
\(\frac{n}{a\left(a+n\right)}=\frac{a+n-a}{a\left(a+n\right)}=\frac{a+n}{a\left(a+n\right)}-\frac{a}{a\left(a+n\right)}=\frac{1}{a}-\frac{1}{a+n}\) ( từ tích thành hiệu )
Tương tự như vậy đối với :
\(\frac{2}{x\left(x+2\right)}=\frac{x+2-x}{x\left(x+2\right)}=\frac{x+2}{x\left(x+2\right)}-\frac{x}{x\left(x+2\right)}=\frac{1}{x}-\frac{1}{x+2}\) ( từ tích thành hiệu )
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
a. Chứng minh rằng: Với mọi giá trị của tham số m phương trình \(\left(1-m^2\right)x^3-6x=1\) luôn có nghiệm
b. CMR với mọi GT của tham số m phương trình \(\left(m^2+m+5\right)\left(3-x\right)^{2021}.x+x-4=0\) luôn có nghiệm
Thầy bày em phương pháp giải dạng này được ko ạ . Em cảm ơn nhiều
Tìm 2 giá trị của x để hàm \(f\left(x\right)\) nhận kết quả trái dấu là được.
a.
Đặt \(f\left(x\right)=\left(1-m^2\right)x^3-6x-1\)
Hàm \(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=-1< 0\) (chọn \(x=0\) do nó làm triệt tiêu tham số m, thường sẽ ưu tiên chọn những giá trị x kiểu thế này. Ở câu này, có đúng 1 giá trị x khiến m triệt tiêu nên phải chọn thêm)
\(f\left(-1\right)=m^2-1+6-1=m^2+4>0\) với mọi m (để ý rằng ta đã có \(f\left(0\right)\) âm nên cần chọn x sao cho \(f\left(x\right)\) dương, mà \(-m^2\) nên ta nên chọn x sao cho nó chuyển dấu thành \(m^2\))
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0;\forall m\)
\(\Rightarrow\) Hàm luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\) với mọi m
Hay với mọi m thì pt luôn luôn có nghiệm
Đúng 2
Bình luận (0)
b.
Đặt \(f\left(x\right)=\left(m^2+m+5\right)\left(3-x\right)^{2021}x+x-4\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=-4< 0\)
(Tới đây, nếu ta chọn tiếp \(x=3\) để triệt tiêu m thì cho \(f\left(3\right)=-1\) vẫn âm, ko giải quyết được vấn đề, nên ta phải chọn 1 giá trị khác. Thường trong những trường hợp xuất hiện \(m^2\) thế này, cố gắng chọn x sao cho hệ số của \(m^2\) dương (nếu cần \(f\left(x\right)\) dương, còn cần \(f\left(x\right)\) âm thì chọn x sao cho hệ số \(m^2\) âm). Ở đây dễ nhất là chọn \(x=2\) , vì khi đó \(\left(3-2\right)^{2021}=1\) vừa đảm bảo hệ số \(m^2\) dương vừa dễ tính toán, nếu chọn \(x=1\) cũng được thôi nhưng quá to sẽ rất khó biến đổi)
\(f\left(2\right)=\left(m^2+m+5\right).\left(3-2\right)^{2021}.2+2-4=2\left(m^2+m+5\right)-2\)
\(=2m^2+2m+8=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{15}{2}>0;\forall m\)
\(\Rightarrow f\left(0\right).f\left(2\right)< 0;\forall m\Rightarrow\) hàm luôn có ít nhất 1 nghiệm thuộc \(\left(0;2\right)\) với mọi m
Hay pt đã cho luôn có nghiệm với mọi m
Đúng 1
Bình luận (0)
Câu 8 : Cho biểu thức :
\(N=\left(\frac{x-1}{\left(x-1\right)^2+x}-\frac{2}{x-2}\right):\left(\frac{\left(x-1\right)^4+2}{\left(x-1\right)^3-1}-x+1\right)\)
Chứng minh rằng với mọi giá trị thích hợp của x thì giá trị N luôn là số nguyên
Câu 8 :
\(N=\left(\frac{x-1}{\left(x-1\right)^2+x}-\frac{2}{x-2}\right):\left(\frac{\left(x-1\right)^4+2}{\left(x-1\right)^3-1}-x+1\right)\)
Đặt \(x-1=a\)
\(N=\left(\frac{a}{a^2+x}-\frac{2}{a-1}\right):\left(\frac{a^4+2}{a^3-1}-a\right)\)
\(N=\frac{a\left(a-1\right)-2\left(a^2+x\right)}{\left(a^2+x\right)\left(a-1\right)}:\frac{a^4+2-a\left(a^3-1\right)}{a^3-1}\)
\(N=\frac{a^2-a-2a^2-2x}{\left(a^2+x\right)\left(a-1\right)}:\frac{a^4+2-a^4+a}{a^3-1}\)
\(N=\frac{-a^2-a-2x}{\left(a^2+x\right)\left(a-1\right)}\cdot\frac{\left(a-1\right)\left(a^2+a+1\right)}{2+a}\)
\(N=\frac{-\left(a^2+a+2x\right)\left(a^2+a+1\right)}{\left(a^2+x\right)\left(2+a\right)}\)
\(N=\frac{-\left[\left(x-1\right)^2+x-1+2x\right]\left[\left(x-1\right)^2+x-1+1\right]}{\left[\left(x-1\right)^2+x\right]\left(2+x-1\right)}\)
\(N=\frac{-\left(x^2+x\right)\left(x^2-x+1\right)}{\left(x^2-x+1\right)\left(x+1\right)}\)
\(N=\frac{-x\left(x+1\right)}{x+1}\)
\(N=-x\)( đpcm )
Đúng 0
Bình luận (0)
Câu 9 : Tìm giá trị nhỏ nhất của biểu thức :
\(P=\frac{x^2}{x+4}\cdot\left(\frac{x^2+16}{x}+8\right)+9\)
Bài làm :
\(P=\frac{x^2}{x+4}\cdot\frac{x^2+8x+16}{x}+9\)
\(P=\frac{x^2\left(x+4\right)^2}{x\left(x+4\right)}+9\)
\(P=x\left(x+4\right)+9\)
\(P=x^2+4x+9\)
\(P=\left(x+2\right)^2+5\ge5\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x=-2\)
Đúng 0
Bình luận (0)
Bài 10 : Tìm GTLN
\(Q=\left(\frac{x^3+8}{x^3-8}\cdot\frac{4x^2+8x+16}{x^2-4}-\frac{4x}{x-2}\right):\frac{-16}{x^4-6x^3+12x^2-8x}\)
\(Q=\left[\frac{\left(x+2\right)\left(x^2-2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\cdot\frac{4\left(x^2+2x+4\right)}{\left(x-2\right)\left(x+2\right)}-\frac{4x}{x-2}\right]:\frac{-16}{x\left(x^3-6x^2+12x-8\right)}\)
\(Q=\left(\frac{4\left(x^2-2x+4\right)}{\left(x-2\right)^2}-\frac{4x\left(x-2\right)}{\left(x-2\right)^2}\right):\frac{-16}{x\left[x^2\left(x-2\right)-4x\left(x-2\right)+4\left(x-2\right)\right]}\)
\(Q=\frac{4x^2-8x+16-4x^2+8x}{\left(x-2\right)^2}:\frac{-16}{x\left(x-2\right)\left(x^2-4x+4\right)}\)
\(Q=\frac{16}{\left(x-2\right)^2}\cdot\frac{-x\left(x-2\right)\left(x-2\right)^2}{16}\)
\(Q=-x\left(x-2\right)\)
\(Q=-x^2+2x\)
\(Q=-x^2+2x-1+1\)
\(Q=1-\left(x-1\right)^2\le1\forall x\)
Dấu "=" \(\Leftrightarrow x=1\)
Vậy....
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
P=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{8\sqrt{x}+8}{x+2\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}}\right):\left(\dfrac{x+\sqrt{x}+3}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}}\right)\)
a. rút gọn P
b. chứng minh rằng với mọi giá trị x ta luôn có P\(\le1\)
\(a,=\dfrac{x+8\sqrt{x}+8-\left(\sqrt{x+2}\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}:\dfrac{x+\sqrt{x}+3+\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+8\sqrt{x}+8-x-4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{2\sqrt{x}+x+5}\)
\(=\dfrac{4\sqrt{x}-4}{2\sqrt{x}+x+5}\)
Vậy \(P=\dfrac{4\sqrt{x}-4}{2\sqrt{x}+x+5}\)
Đúng 1
Bình luận (0)