Trong mặt phẳng Oxy cho hình bình hành ABCD với A(2;4), B(-3;1), C(3;-1) và D(8;2).
a/ Tính tọa độ chân A' của đường cao vẽ từ đỉnh A của tam giác ABC
b/ Tính diện tích của hình bình hành ABCD
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(-2; 0); B(2; 5); C( 6; 2).Tìm tọa độ điểm D?
A. D(2; -3)
B. D(2; 3)
C. D(-2; -3)
D. D(-2; 3)
Gọi D(x; y)
Ta có A D → = x + 2 ; y và B C → = 4 ; − 3 .
Vì ABCD là hình bình hành nên A D → = B C →
x + 2 = 4 y = − 3 ⇔ x = 2 y = − 3 ⇒ D 2 ; − 3 .
Chọn A.
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. D( -8; 5).
B. D( 5; 8).
C. D( 8; 5).
D. D( 8; -5).
Chọn D.
Ta có: tứ giác ABCD là hình bình hành khi

Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A.D( -8; 5)
B. D( 5; 8)
C.D( 8; 5)
D.D( 8; -5) .
Ta có: tứ giác ABCD là hình bình hành khi
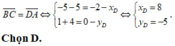
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 5: Trong mặt phẳng toạ độ Oxy cho A(3;-1) ; B(-1;2) ; và I(1;1). Xác định toạ độ điểm C, D sao cho tứ giác ABCD là hình bình hành biết I là trong tâm tam giác ABC. Tìm toạ tâm O của hình bình hành ABCD
I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(1;3); B(-1;-2).Tìm tọa độ điểm M trên Oy sao cho A,B,D thẳng hàng
GẤP Ạ
Chắc là A,B,M thẳng hàng chứ?
Do M thuộc Oy nên tọa độ có dạng: \(M\left(0;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BA}=\left(2;5\right)\\\overrightarrow{BM}=\left(1;m+2\right)\end{matrix}\right.\)
A, B, M thẳng hàng \(\Rightarrow\overrightarrow{BA}\) cùng phương \(\overrightarrow{BM}\)
\(\Rightarrow\dfrac{1}{2}=\dfrac{m+2}{5}\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow M\left(0;\dfrac{1}{2}\right)\)
Trong mặt phẳng oxy cho 3 điểm A(-5;2) B(4:-3) C(6:1) tìm tọa độ D để tứ giác abcd là hình bình hành
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(9;-5\right)\\\overrightarrow{CD}=\left(6-x;1-y\right)\end{matrix}\right.\)
ABCD là hình bình hành khi \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}6-x=9\\1-y=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(-3;6\right)\)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A (3;2) , B(-4;2) ,C (3;5) tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành
vecto AB=(-7;0)
vecto DC=(3-x;5-y)
Vì ABCD là hình bình hành
nên vecto AB=vecto DC
=>3-x=-7; 5-y=0
=>x=10; y=5