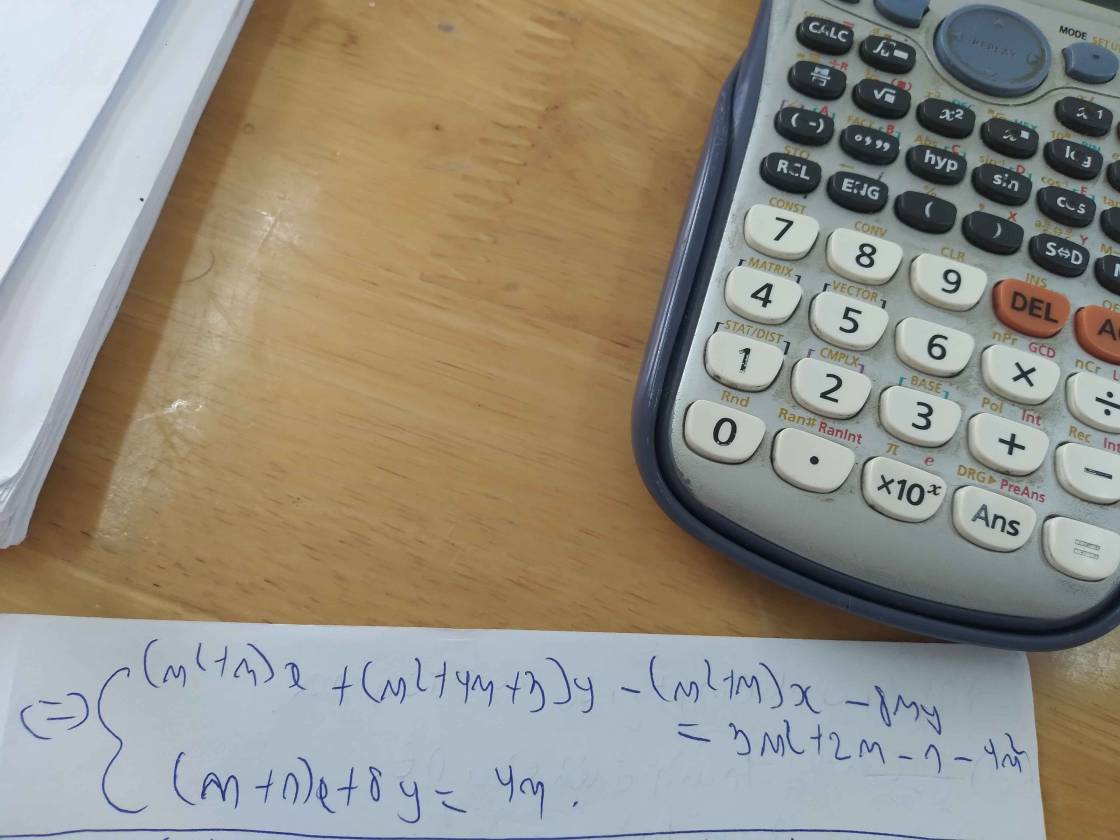Tìm m để hệ pt trên có nghiệm duy nhất (z;y;z) sao cho x2 +y2+z2 đạt giá trị nhỏ nhất?
ND
Những câu hỏi liên quan
\(\left\{{}\begin{matrix}x+y+\left(m+1\right)z=2\\3x+4y+2z=m+1\\2x+3y-z=1\end{matrix}\right.\). Tìm m để pt vô số nghiệm
Lần lượt lấy pt (3) trừ 2 lần pt (1) và pt (2) trừ 3 lần pt (1) ta được:
\(\left\{{}\begin{matrix}y-\left(2m+3\right)z=-3\\y-\left(3m+1\right)z=m-3\end{matrix}\right.\)
Hệ đã cho có vô số nghiệm khi và chỉ khi:
\(\dfrac{1}{1}=\dfrac{3m+1}{2m+3}=\dfrac{m-3}{-3}\) (ko tồn tại m thỏa mãn)
Vậy ko tồn tại m để hệ có vô số nghiệm
Đúng 0
Bình luận (0)
Cho \(\left\{{}\begin{matrix}x +my=2\\mx-2y=1\end{matrix}\right.\)a) tìm \(m\in Z\) để hệ có nghiệm duy nhất (x; y) sao cho x lớn hơn 0 và y lớn hơn 0 b) tìm \(m\in Z\) để hệ có nghiệm duy nhất (x; y) sao cho (x; y) nguyên
a) Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+m^2y=2m\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2y+2y=2m-1\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2+2\right)=2m-1\\mx=1+2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m-1}{m^2+2}\\x=\dfrac{1+2y}{m}=\left(1+\dfrac{2m-1}{m^2+2}\right)\cdot\dfrac{1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2+2+2m-1}{m^2+2}\cdot\dfrac{1}{m}=\dfrac{m^2+2m+1}{m\left(m^2+2\right)}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{m^2+2m+1}{m\left(m^2+2\right)}>0\\\dfrac{2m-1}{m^2+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m>\dfrac{1}{2}>0\)
Vậy: Khi m>0 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x>0 và y>0
Đúng 0
Bình luận (1)
bài 1 : cho hệ ptleft{{}begin{matrix}3x+2y5x+my2end{matrix}right.
1. Tìm m để hệ có nghiệm duy nhất thỏa mãn x-y 2
2. tìm m inz để hệ có nghiệm duy nhất xinz , yinz
3. Tìm m để hệ có nghiệm duy nhất ( x;y) ingóc phần tư thứ 3
Bài 2 : cho hệ pt left{{}begin{matrix}x+y3mx-2y-3end{matrix}right.
1. Tìm m để hệ có nghiệm duy nhất thỏa mãn x^2 + xy 30
MỌI NGƯỜI GIÚP EM VỚI Ạ !!!
Đọc tiếp
bài 1 : cho hệ pt\(\left\{{}\begin{matrix}3x+2y=5\\x+my=2\end{matrix}\right.\)
1. Tìm m để hệ có nghiệm duy nhất thỏa mãn x-y = 2
2. tìm m \(\in\)z để hệ có nghiệm duy nhất x\(\in\)z , y\(\in\)z
3. Tìm m để hệ có nghiệm duy nhất ( x;y) \(\in\)góc phần tư thứ 3
Bài 2 : cho hệ pt \(\left\{{}\begin{matrix}x+y=3m\\x-2y=-3\end{matrix}\right.\)
1. Tìm m để hệ có nghiệm duy nhất thỏa mãn \(x^2\) + xy = 30
MỌI NGƯỜI GIÚP EM VỚI Ạ !!!
cho hệ pt x-2y=3-m (1) 2x+y=3(m+2) (2) a. giải hệ vs m=2 b. tìm tất các giá trị của m để hệ có nghiệm duy nhất c. tìm GTNN của A=x^2+y^2 trong đó x, y là nghiệm duy nhất của hệ d,. tìm m để hệ có nghiệm sao cho 5x-y=3
Cho hệ phương trình hept{begin{cases}mx-2y2m-12x-my9-3mend{cases}}a) tìm m để hệ phương trình có nghiệm duy nhất (x;y) tìm nghiệm duy nhất đób) Với x, y vừa tìm được ở trên +tìm hệ thức liên hệ giữa x, y không phụ thuộc vào m+ tìm m inZ để x, y nguyên+ tìm m để S 2x2 - y2 đạt GTNN+ tìm m để T xy đạt GTLN
Đọc tiếp
Cho hệ phương trình \(\hept{\begin{cases}mx-2y=2m-1\\2x-my=9-3m\end{cases}}\)
a) tìm m để hệ phương trình có nghiệm duy nhất (x;y) tìm nghiệm duy nhất đó
b) Với x, y vừa tìm được ở trên
+tìm hệ thức liên hệ giữa x, y không phụ thuộc vào m
+ tìm m \(\in\)Z để x, y nguyên
+ tìm m để S = 2x2 - y2 đạt GTNN
+ tìm m để T = xy đạt GTLN
b1 : cho hệ pt (m-1)x - my 3m-1 2x-y m+5a) giải hệ pt khi m 2b) tìm m để hệ pt có nghiệm duy nhất sao cho x^2 -y^24
b2 : cho hệ pt mx + y 1 x + my m + 1với gtrị nào của m thì hệ pt có nghiệm duy nhấtvới gtrị nào của m thì hệ pt có vô số nghiệmvới gtrị nào của m thì hệ pt vô nghiệm
Đọc tiếp
b1 : cho hệ pt (m-1)x - my = 3m-1
2x-y =m+5
a) giải hệ pt khi m = 2
b) tìm m để hệ pt có nghiệm duy nhất sao cho \(x^2 -y^2=4 \)
b2 : cho hệ pt mx + y = 1
x + my = m + 1
với gtrị nào của m thì hệ pt có nghiệm duy nhất
với gtrị nào của m thì hệ pt có vô số nghiệm
với gtrị nào của m thì hệ pt vô nghiệm
Thay m=2 vào HPT ta có:
\(\left\{{}\begin{matrix}\left(2-1\right)x-2y=6-1\\2x-y=2+5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x-2y=5\\2x-y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x-4y=10\\2x-y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x-4y=10\\-3y=3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
Vậy HPT có nghiemj (x;y) = (3;-11)
Đúng 1
Bình luận (1)
cho hệ pt x+my=2 và mx+y=3 với m là tham số. tìm m để pt có nghiệm duy nhất thỏa mãn 2x+y=5/2
Giải các hệ pt, bất pt sau:
a, \(\left\{{}\begin{matrix}2x-2y+z=3\\2x+y-2z=-3\\3x-4y-z=4\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}2x-3y\ge2\\3x+2y< 4\\x-2y\ge5\end{matrix}\right.\)
a: \(\left\{{}\begin{matrix}2x-2y+z=3\\2x+y-2z=-3\\3x-4y-z=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-4y+2z=6\\8x+4y-8z=-3\\3x-4y-z=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-6z=3\\11x-9z=1\\3x-4y-z=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\z=\dfrac{1}{2}\\4y=3x-z-4=\dfrac{3}{2}-\dfrac{1}{2}-4=1-4=-3\end{matrix}\right.\)
=>x=1/2;z=1/2;y=-3/4
Đúng 1
Bình luận (1)
Cho hệ phương trình (m+1)x +8y =4m
mx + (m+3)y=3m-1
tìm m nguyên để hpt có nghiệm duy nhất (x;y) thỏa mãn x,y ϵ Z
Giải hệ phương trình:
\(\hept{\begin{cases}x+2my-z=1\\2x-my-2z=2\\x-\left(m+4\right)y-z=1\end{cases}}\)
có nghiệm (x;y;z) với m khác 0 và -4/3