cau c ạ

Cau 9 vs cau 10 ạ
giúp em cau c voi cac thầy ơi... em cảm ơn nhieu ạ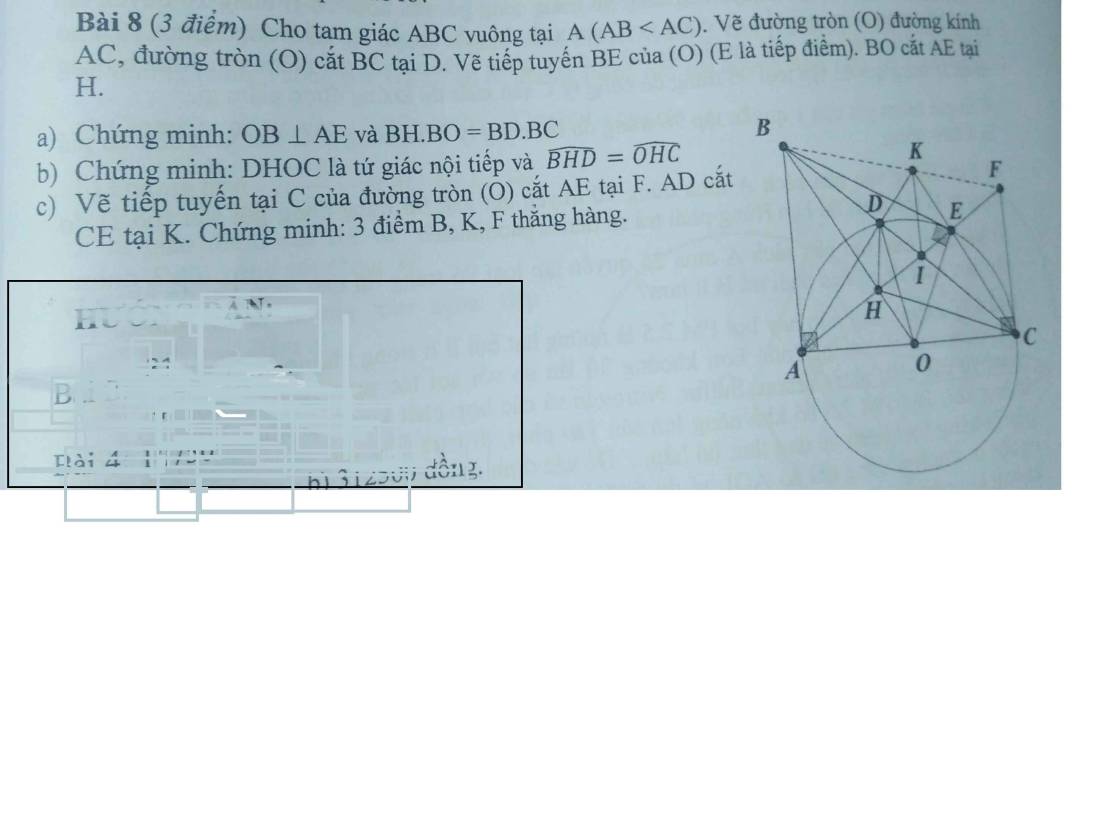
Mn ơi chỉ em cau C thôi,mn giải em chi tiết với ạ hihi,em cảm ơn mọi người nhìu
a: AC=4cm
AH=2,4cm
BH=1,8cm
CH=3,2cm
![]() giúp em cau này với ạ Giá trị của biểu thức 2x biết x 8 là
giúp em cau này với ạ Giá trị của biểu thức 2x biết x 8 là
A.16 . B. 16. C. 4 . D. 10
.
Giúp e cau 9,10,11 ạ
\(9,\tan B=\dfrac{AC}{AB}=\dfrac{4}{3}\left(B\right)\\ 10,A=\dfrac{x-4\sqrt{x}+4\sqrt{x}+16}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\dfrac{\sqrt{x}+4}{x+16}\\ A=\dfrac{x+16}{\left(\sqrt{x}-4\right)\left(x+16\right)}=\dfrac{1}{\sqrt{x}-4}\left(A\right)\\ 11,B=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(x-1\right)^2}{2}\\ B=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)^2}{2}\\ B=\dfrac{-2\sqrt{x}\left(\sqrt{x}-1\right)}{2}=-\sqrt{x}\left(\sqrt{x}-1\right)\\ B>0\Leftrightarrow\sqrt{x}-1< 0\left(-\sqrt{x}< 0\right)\\ \Leftrightarrow0\le x< 1\left(D\right)\)
Giup minh cau 9 ạ
giúp mình với ạ cau 1,2,3,4,5
Giải giúp em cau 2 vs ạ
Mọi người giải em hộ bài
3.9 cau a, b, d, và h
3.10 cau a, b, e, và c
e Cảm ơn nhiều ạ
Bài 3.9:
a)
\(\int ^{1}_{0}(y^3+3y^2-2)dy=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\left ( \frac{y^4}{4}+y^3-2y \right )=\frac{-3}{4}\)
b) \(\int ^{4}_{1}\left (t+\frac{1}{\sqrt{t}}-\frac{1}{t^2}\right)dt=\left.\begin{matrix} 4\\ 1\end{matrix}\right|\left ( \frac{t^2}{2}+2\sqrt{t}+\frac{1}{t} \right )=\frac{35}{4}\)
d) Ta có:
\(\int ^{1}_{0}(3^s-2^s)^2ds=\int ^{1}_{0}(9^s+4^s-2.6^s)ds=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\left ( \frac{9^s}{\ln 9}+\frac{4^s}{\ln 4}-\frac{2.6^s}{\ln 6} \right )\)
\(=\frac{8}{\ln 9}+\frac{3}{\ln 4}-\frac{10}{\ln 6}\)
h)
Ta có \(\int ^{\frac{5\pi}{4}}_{\pi}\frac{\sin x-\cos x}{\sqrt{1+\sin 2x}}dx=\int ^{\frac{5\pi}{4}}_{\pi}\frac{\sin x-\cos x}{\sqrt{\sin^2x+\cos^2x+2\sin x\cos x}}dx\)
\(=\int ^{\frac{5\pi}{4}}_{\pi}\frac{-d(\sin x+\cos x)}{|\sin x+\cos x|}=\int ^{\frac{5\pi}{4}}_{\pi}\frac{d(\sin x+\cos x)}{\sin x+\cos x}=\left.\begin{matrix} \frac{5\pi}{4}\\ \pi\end{matrix}\right|\ln |\sin x+\cos x|=\ln (\sqrt{2})\)
Bài 3.10:
a)
Đặt \(t=1-x\) thì:
\(\int ^{2}_{1}x(1-x)^5dx=\int ^{-1}_{0}t^5(1-t)d(1-t)=\int ^{0}_{-1}t^5(1-t)dt\)
\(=\left.\begin{matrix} 0\\ -1\end{matrix}\right|\left ( \frac{t^6}{6}-\frac{t^7}{7} \right )=\frac{-13}{42}\)
b) Đặt \(\sqrt{e^x-1}=t\) \(\Rightarrow x=\ln (t^2+1)\)
Khi đó
\(\int ^{\ln 2}_{0}\sqrt{e^x-1}dx=\int ^{1}_{0}td(\ln (t^2+1))=\int ^{1}_{0}t.\frac{2t}{t^2+1}dt\)
\(=\int ^{1}_{0}\frac{2t^2}{t^2+1}dt=\int ^{1}_{0}2dt-\int ^{1}_{0}\frac{2}{t^2+1}dt=\left.\begin{matrix} 1\\ 0\end{matrix}\right|2t-\int ^{1}_{0}\frac{2dt}{t^2+1}=2-\int ^{1}_{0}\frac{2dt}{t^2+1}\)
Với \(\int ^{1}_{0}\frac{2dt}{t^2+1}\), đặt \(t=\tan m\)
\(\Rightarrow \int ^{1}_{0}\frac{2dt}{t^2+1}=\int ^{\frac{\pi}{4}}_{0}\frac{2d(\tan m)}{\tan ^2m+1}=\int ^{\frac{\pi}{4}}_{0}2\cos ^2md(\tan m)\)
\(=\int ^{\frac{\pi}{4}}_{0}2dm=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|2m=\frac{\pi}{2}\)
Do đó \(\int ^{\ln 2}_{0}\sqrt{e^x-1}dx=2-\frac{\pi}{2}\)
Bài 3.10
c) Đặt \(t=\sqrt[3]{1-x}\Rightarrow x=1-t^3\)
\(\int ^{9}_{1}x\sqrt[3]{1-x}dx=\int ^{-2}_{0}(1-t^3)td(1-t^3)=\int ^{0}_{-2}3t^2.t(1-t^3)dt\)
\(\left.\begin{matrix} 0\\ -2\end{matrix}\right|\left ( \frac{3t^4}{4}-\frac{3t^7}{7} \right )=\frac{-468}{7}\)
e) Đặt \(t=\frac{1}{x}\) suy ra:
\(\int ^{2}_{1}\frac{\sqrt{x^2+1}}{x^4}dx=\int ^{\frac{1}{2}}_{1}t^4\sqrt{\frac{1}{t^2}+1}d\left(\frac{1}{t}\right)\)
\(=\int ^{1}_{\frac{1}{2}}\frac{t^4\sqrt{t^2+1}}{t}.\frac{1}{t^2}dt=\int ^{1}_{\frac{1}{2}}t\sqrt{t^2+1}dt=\frac{1}{2}\int ^{1}_{\frac{1}{2}}\sqrt{t^2+1}d(t^2+1)\)
\(=\left.\begin{matrix} 1\\ \frac{1}{2}\end{matrix}\right|\left(\frac{1}{2}.\frac{2}{3}\sqrt{(t^2+1)^3}\right)=\frac{2\sqrt{2}}{3}-\frac{5\sqrt{5}}{24}\)