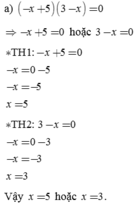Số giá trị của x thỏa mãn (x2+1)(x2+5)=0
TA
Những câu hỏi liên quan
Giá trị nào của số nguyên x, thỏa mãn:
a) ( - x + 5 ) ( 3 - x ) = 0
b) ( x - 1 ) x 2 + 1 = 0
Tìm giá trị của m để phương trình
x
2
– 2(m – 2)x + 2m – 5 0 hai nghiệm
x
1
;
x
2
thỏa mãn
x
1
(
1
−
x
2
)
+
x
2
(
2
–
x
1
)...
Đọc tiếp
Tìm giá trị của m để phương trình x 2 – 2(m – 2)x + 2m – 5 = 0 hai nghiệm x 1 ; x 2 thỏa mãn x 1 ( 1 − x 2 ) + x 2 ( 2 – x 1 ) < 4
A. m > 1
B. m < 0
C. m > 2
D. m < 3
Phương trình x 2 – 2(m – 2)x + 2m – 5 = 0 có a = 1 ≠ 0 và
∆ ' = ( m − 2 ) 2 – 2 m + 5 = m 2 – 6 m + 9 = ( m – 3 ) 2 ≥ 0 ; ∀ m
Nên phương trình luôn có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m − 4 x 1 . x 2 = 2 m − 5
X é t x 1 ( 1 − x 2 ) + x 2 ( 2 – x 1 ) < 4 ⇔ ( x 1 + x 2 ) – 2 x 1 . x 2 − 4 < 0
⇔ 2m – 4 – 2(2m – 5) – 4 < 0 ⇔ −2m + 2 < 0 m > 1
Vậy m > 1 là giá trị cần tìm
Đáp án: A
Đúng 0
Bình luận (0)
cho phương trình x2 - 2 (m - 1)x - 2m + 5 = 0 (m là tham số)
tính các giá trị của m để phương trình có 2 nghiệm phân biệt x1 , x2 (x1 < x2) thỏa mãn x1 - x2 = -2
Để phương trình 1 có 2 nghiệm phân biệt
=> \(\Delta,>0\) <=> \(\left[-\left(m-1\right)\right]^2-\left(-2m+5\right)>0\)
<=>\(\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)
=> Theo hệ thức Vi ét ta có
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\circledast\\x_1.x_2=-2m+5\circledast\circledast\end{matrix}\right.\)
Theo bài ra ta có
\(x_1-x_2=-2\circledcirc\)
Từ \(\circledast vaf\circledcirc\) ta có hệ pt
\(\left\{{}\begin{matrix}x1+x2=2m-2\\x1-x2=-2\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}x1=m-2\\x2=m\end{matrix}\right.\)
Thay x1 và x2 vào \(\circledast\circledast\)ta dc
\(\left(m-2\right)m=-2m+5\)
<=> m=\(\left[{}\begin{matrix}-\sqrt{5}\\\sqrt{5}\end{matrix}\right.\left(tm\right)\)
Vậy ...
Đúng 1
Bình luận (0)
Cho phương trình x2 + 2(m - 1)x - 2m + 5 =0 ( m là tham số). Tìm giá trị của m để phương trình có hai nghiệm x1; x2 thỏa mãn 2x1 + 3x2 = -5
Lời giải:
Để pt có 2 nghiệm thì:
$\Delta'=(m-1)^2+2m-5\geq 0$
$\Leftrightarrow m^2-4\geq 0$
$\Leftrightarrow m\geq 2$ hoặc $m\leq -2$
Áp dụng định lý Viet: \(\left\{\begin{matrix}
x_1+x_2=2(1-m)\\
x_1x_2=-2m+5\end{matrix}\right.\)
\(2x_1+3x_2=-5\)
\(\Leftrightarrow 2(x_1+x_2)+x_2=-5\Leftrightarrow 4(1-m)+x_2=-5\)
\(\Leftrightarrow x_2=4m-9\)
\(x_1=2(1-m)-x_2=11-6m\)
$x_1x_2=-2m+5$
$\Leftrightarrow (4m-9)(11-6m)=-2m+5$
Giải pt này suy ra $m=2$ hoặc $m=\frac{13}{6}$ (đều thỏa mãn)
Đúng 1
Bình luận (0)
Cho
x
1
v
à
x
2
(
x
1
x
2
)
là hai giá trị thỏa mãn x(3x – 1) – 5(1 – 3x) 0. Khi đó
3
x
1
-
x
2
bằng A. -4 B. 4 C. 6 D. -6
Đọc tiếp
Cho x 1 v à x 2 ( x 1 > x 2 ) là hai giá trị thỏa mãn x(3x – 1) – 5(1 – 3x) = 0. Khi đó 3 x 1 - x 2 bằng
A. -4
B. 4
C. 6
D. -6
Ta có x(3x – 1) – 5(1 – 3x) = 0
ó x(3x – 1) + 5(3x – 1) = 0 ó (3x – 1)(x + 5) = 0
ó x + 5 = 0 3 x - 1 = 0 ó x = - 5 3 x = 1 ó x = - 5 x = 1 3
Suy ra
x 1 = 1 3 ; x 2 = - 5 ⇒ 3 x 1 - x 2 = 3 . 1 3 - - 5 = 6
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để pt: (m + 1).25log2(x) + (m - 2)xlog2(5) - 2m + 1 = 0 có 2 nghiệm phân biệt x1, x2 thỏa mãn: x1.x2 = 4
ĐKXĐ: \(x>0\)
\(x^{log_25}=t\Rightarrow25^{log_2x}=\left(5^{log_2x}\right)^2=\left(x^{log_25}\right)^2=t^2\)
\(x_1x_2=4\Rightarrow t_1t_2=\left(x_1x_2\right)^{log_25}=4^{log_25}=25\)
\(\left(m+1\right)t^2+\left(m-2\right)t-2m+1=0\) (1)
Pt có 2 nghiệm pb \(\Rightarrow\) (1) có 2 nghiệm dương pb
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-2\right)^2-4\left(m+1\right)\left(-2m+1\right)>0\\t_1+t_2=\dfrac{2-m}{m+1}>0\\t_1t_2=\dfrac{-2m+1}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\-1< m< \dfrac{1}{2}\end{matrix}\right.\)
Ủa làm đến đây mới thấy kì kì, chỉ riêng hệ điều kiện này đã ko tồn tại m nguyên rồi, chưa cần điều kiện \(x_1x_2=4\)
Đúng 0
Bình luận (1)
\(t=1\) pt có nghiệm kép bạn ơi, ko phải 2 nghiệm pb như đề yêu cầu đâu
Đúng 0
Bình luận (0)
Cho phương trình x2 - (2m+5)x +2m + 1 = 0 với m là tham số có 2 nghiệm dương phân biệt x1,x2 . Tìm m thỏa mãn ∣∣√x1−√x2∣∣|x1−x2| có giá trị nhỏ nhất.
Cho phương trình :
x2 − 2x + 2 − m = 0 (x là ẩn số, m là tham số)
Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn hệ thức:
2x13 +(m + 2)x2 2 = 5
Lời giải:
Để pt có 2 nghiệm pb thì:
$\Delta'=1-(2-m)=m-1>0\Leftrightarrow m>1$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=2-m\end{matrix}\right.\)
Khi đó:
$2x_1^3+(m+2)x_2^2=5$
$\Leftrightarrow 2x_1^3+(2x_1+2x_2-x_1x_2)x_2^2=5$
$\Leftrightarrow 2(x_1^3+x_2^3)+x_1(2-x_2)x_2^2=5$
\(\Leftrightarrow 2[(x_1+x_2)^3-3x_1x_2(x_1+x_2)]+x_1^2x_2^2=5\)
\(\Leftrightarrow 2[8-6(2-m)]+(2-m)^2=5\)
\(\Leftrightarrow m^2+8m-9=0\Leftrightarrow (m-1)(m+9)=0\)
Vì $m>1$ nên không có giá trị nào của $m$ thỏa mãn.
Đúng 2
Bình luận (7)
cho phương trình bậc hai x2-2(m-1)x+2m-5=0 (1)
với giá trị nào của m thì phương trình có hai nghiệm x1,x2 thỏa mãn:
x1<2<x2
Để phương trình (1) có nghiệm thì:
\(\Delta'\ge0\Rightarrow\left(m-1\right)^2-\left(2m-5\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-2m+5\ge0\)
\(\Leftrightarrow\left(m-2\right)^2+2\ge0\) (luôn đúng)
Vậy với \(\forall m\) thì phương trình (1) luôn có nghiệm.
Theo định lí Vi-et cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
Ta có: \(x_1< 2< x_2\Rightarrow\left\{{}\begin{matrix}x_1-2< 0\\x_2-2>0\end{matrix}\right.\)
\(\Rightarrow\left(x_1-2\right)\left(x_2-2\right)< 0\)
\(\Rightarrow x_1x_2-2\left(x_1+x_2\right)+4< 0\)
\(\Rightarrow2m-5-2.2\left(m-1\right)+4< 0\)
\(\Rightarrow2m-5-4m+4+4< 0\)
\(\Rightarrow-2m+3< 0\)
\(\Rightarrow m>\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Với tất cả giá trị nào của tham số m thì phương trình
(
m
-
10
)
x
2
-
2
(
m
-
2
)
x
+
m
-
3
0
có hai nghiệm
x
1
,
x
2
thỏa mãn
x
1
+
x...
Đọc tiếp
Với tất cả giá trị nào của tham số m thì phương trình ( m - 10 ) x 2 - 2 ( m - 2 ) x + m - 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 + x 1 . x 2 < 1
A. 1<m<3.
B. 1<m<2.
C. m>2.
D. m>3.