NT
Những câu hỏi liên quan
giúp mình câu c bài 1 và cả bài 2 với ạ
Đọc tiếp
giúp mình câu c bài 1 và cả bài 2 với ạ
Bài 1:
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy
Đúng 3
Bình luận (0)
Giúp mình bài 1 câu a và hết bài 2 với ạ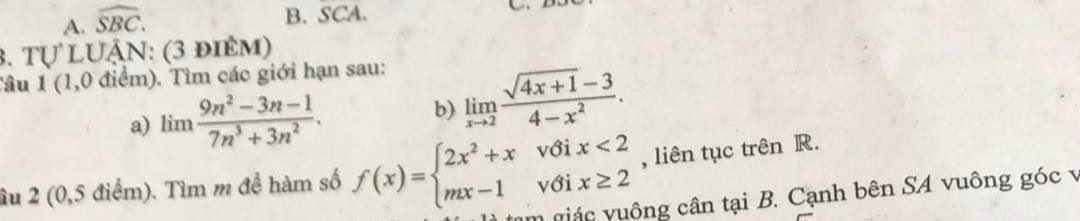
Câu 1 : a . \(lim\dfrac{9n^2-3n-1}{7n^3+3n^2}=lim\dfrac{\dfrac{9}{n}-\dfrac{3}{n^2}-\dfrac{1}{n^3}}{7+\dfrac{3}{n}}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{4x+1}-3}{4-x^2}=lim_{x\rightarrow2}\dfrac{4x+1-9}{\left(\sqrt{4x+1}+3\right)\left(4-x^2\right)}\)
\(=lim_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(\sqrt{4x+1}+3\right)\left(2-x\right)\left(2+x\right)}\)
\(=lim_{x\rightarrow2}\dfrac{-4}{\left(\sqrt{4x+1}+3\right)\left(2+x\right)}=\dfrac{-4}{\left(3+3\right)\left(2+2\right)}=-\dfrac{1}{6}\)
Đúng 0
Bình luận (0)
Câu 2 : Ta có : f(x) = \(\left\{{}\begin{matrix}2x^2+x\left(x< 2\right)\\mx-1\left(x\ge2\right)\end{matrix}\right.\)
TXĐ : D = R . Với x < 2 ; hàm số liên tục
Với x > 2 ; hàm số liên tục
Với x = 2 , ta có : \(lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^-}2x^2+x=2.2^2+2=10\)
\(lim_{x\rightarrow2^+}f\left(x\right)=lim_{x\rightarrow2^+}mx-1=2m-1\)
Hàm số liên tục trên R <=> Hàm số liên tục tại x = 2
\(\Leftrightarrow lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^+}f\left(x\right)\)
\(\Leftrightarrow10=2m-1\) \(\Leftrightarrow m=\dfrac{11}{2}\)
Vậy ...
Đúng 0
Bình luận (0)
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
Đúng 2
Bình luận (3)
Làm giúp mình 5 câu cuối bài 1 và bài 2 với ạ

6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)
Đúng 0
Bình luận (0)

Giúp mình 3 câu cuối cùng của bài 1 và bài 2 với ạ mình đng cần khá gấp hạn cuối là 15h chiều Hnay ạ
`@` `\text {Ans}`
`\downarrow`

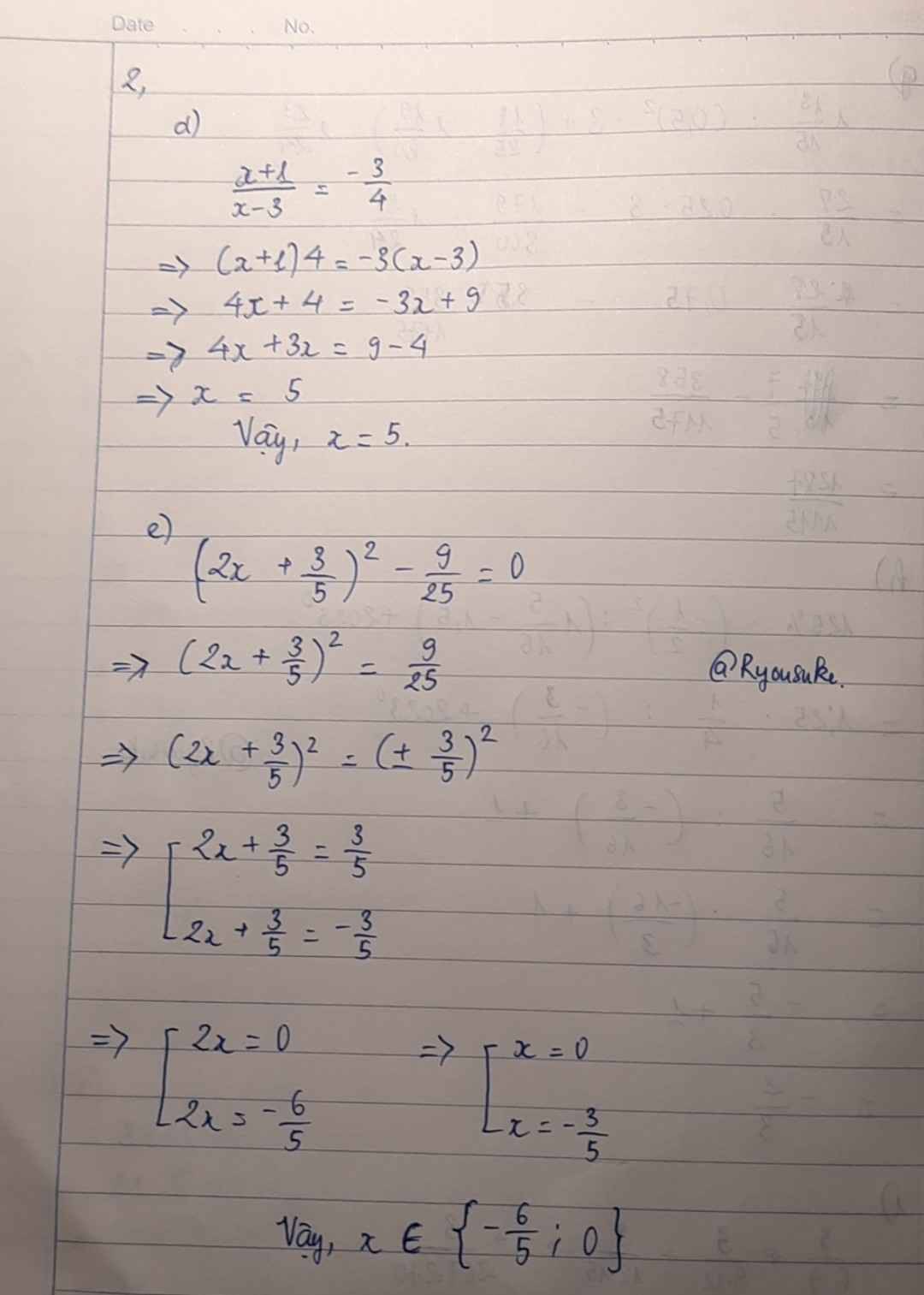
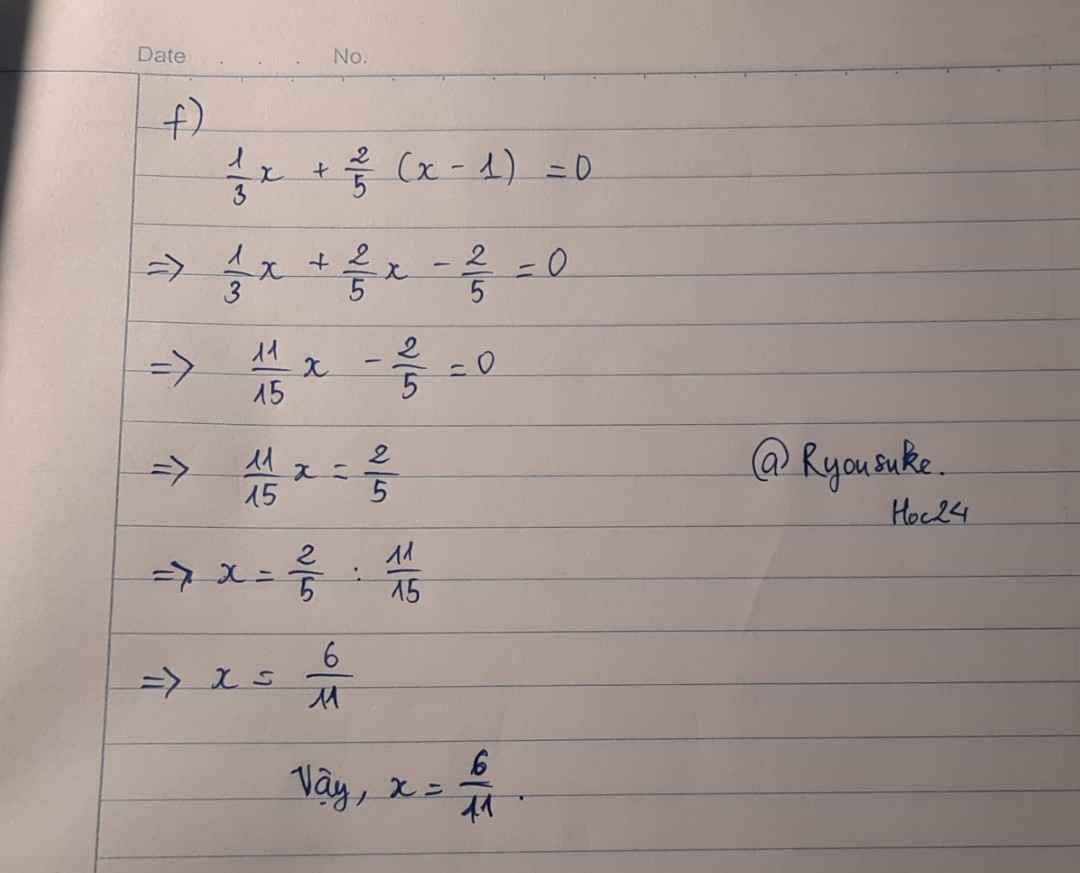
Đúng 2
Bình luận (0)
Hello mng ạ , mng giúp mình kiểm tra mấy bài này làm đúng chưa với ạ và mng giúp luôn mình bài 6 câu 2 ạ
Mình cảm ơn ạ

mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch
Đúng 2
Bình luận (1)
2 have repainted
4 have done
8 have stepped
9 have you ever played
7) 1 riding -walking
2 swimming
3 watching
8)
2 my mother doesn't like listening to music
5 doing more exercises makes you healthier
còn lại ok nha
Đúng 1
Bình luận (1)
chịu ???????????????????
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Đúng 1
Bình luận (1)
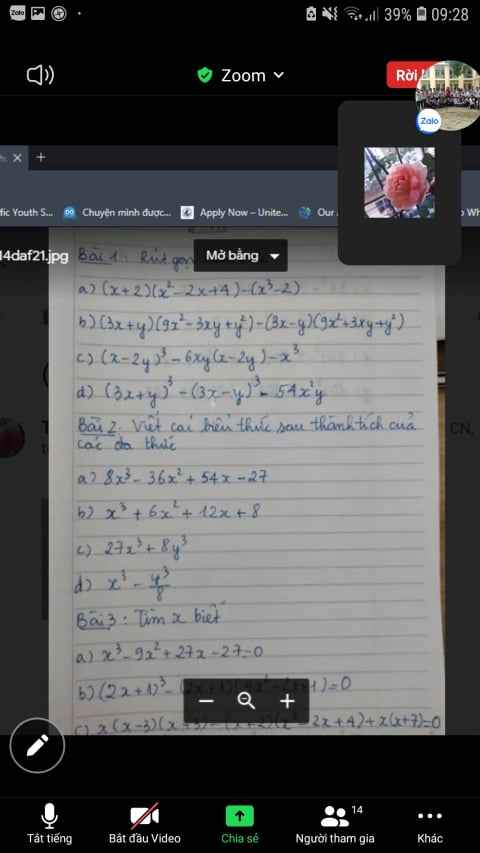
làm giúp mình bài 2 với câu d bài 1 vs ạ
Em hãy đăng bài ở môn Toán nhé!
Đúng 2
Bình luận (1)
Bài 2:
a: \(8x^3-36x^2+54x-27=\left(2x-3\right)^3\)
b: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
c: \(27x^3+8y^3=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
d: \(x^3-\dfrac{y^3}{8}=\left(x-\dfrac{1}{2}y\right)\left(x^2+\dfrac{1}{2}xy+\dfrac{1}{4}y^2\right)\)
Đúng 2
Bình luận (0)
Giúp mình làm Câu c) bài hình và bài cuối với ạ, mình cảm ơn :3
Nhanh một chút ạ, mình đang cần

Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)
Đúng 1
Bình luận (3)
Câu 5:
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\sqrt{1+x}+\sqrt{1-x}=t>0\)
\(\Rightarrow t^2=1+x+1-x+2\sqrt{\left(1+x\right)\left(1-x\right)}=2+2\sqrt{1-x^2}\)
Do đó pt trở thành:
\(t.t^2=8\Leftrightarrow t^3=8\)
\(\Leftrightarrow t=2\Leftrightarrow\sqrt{1-x}+\sqrt{1+x}=2\)
\(\Leftrightarrow2+2\sqrt{1-x^2}=4\Leftrightarrow\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=1\)
\(\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)






