Tìm Min, Max. A = sinα + \(\sqrt{3}\)cosα
H24
Những câu hỏi liên quan
A = \(\dfrac{\text{sinα + cosα}}{\text{sinα - cosα}}\) Tính α biết tan α = \(\sqrt{3}\)
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
Đúng 1
Bình luận (0)
Cho
A
B
C
^
60
0
và ∆ABC tam giác nhọna, Tính sinα, tanα, cotα, biết cosα
1
5
b, Tính cosα, tanα, cotα, biết sinα
2
3
c, Cho tanα 2. Tính sinα, cosα, cotαd, Cho cotα 3. Tính sinα, cosα, tanα
Đọc tiếp
Cho A B C ^ = 60 0 và ∆ABC tam giác nhọn
a, Tính sinα, tanα, cotα, biết cosα = 1 5
b, Tính cosα, tanα, cotα, biết sinα = 2 3
c, Cho tanα = 2. Tính sinα, cosα, cotα
d, Cho cotα = 3. Tính sinα, cosα, tanα
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
Đúng 0
Bình luận (0)
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Biết sinα=\(\dfrac{\sqrt{3}}{2}\).Tính cosα,tanα,cotα?
ta có :\(\sin2=\dfrac{\sqrt{3}}{2}\Rightarrow2=60^0\)
\(\cos60^o=\dfrac{1}{2};\tan60^o=\sqrt{3};\cot60^o=\dfrac{1}{\sqrt{3}}\)
Đúng 0
Bình luận (0)
Bài 1: Biết sinα = \(\dfrac{\sqrt{3}}{2}\). Hãy tính cosα, tanα, cotα.
Bài 2: Biết tanα = 2. Hãy tính sinα, cotα, cosα
Bài 3: Tính: A= cos2 20o + cos2 40o + cos2 50o + cos2 70o
Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2
Đúng 0
Bình luận (0)
Bài 1: Biết rằng sinα = 0,6. Tính cosα và tgα.
Bài 2: Biết rằng cosα = 0,7. Tính sinα và tgα.
Bài 3: Biết rằng tgα = 0,8. Tính sinα và cosα.
Bài 4: Biết cosx = \(\dfrac{1}{2}\), tính P = 3sin2x + 4cos2x.
Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
Đúng 1
Bình luận (0)
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~ Bài 1:Tính giá trị biểu thứca) A sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°b) C cos²52° sin45°+sin²52° cos45°c) E sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°Bài 2: C/m rằng với góc nhọn α ta luôn cóa) (sinα +cosα)²-(sinα -cosα)² 4sinα cosαb) cosα/1-sinα 1+sinα/cosαc) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ sinx+cosxBài 3: Cho α là một góc nhọn a) Biết sinα 3/4. Tính cosα(90°-...
Đọc tiếp
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~
Bài 1:Tính giá trị biểu thức
a) A= sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°
b) C= cos²52° sin45°+sin²52° cos45°
c) E= sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°
Bài 2: C/m rằng với góc nhọn α ta luôn có
a) (sinα +cosα)²-(sinα -cosα)² = 4sinα cosα
b) cosα/1-sinα =1+sinα/cosα
c) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ =sinx+cosx
Bài 3: Cho α là một góc nhọn
a) Biết sinα =3/4. Tính cosα(90°-α)
b) Biết tanα =2. Tính cotα(90°-α)
Cho α là góc nhọn và cosα = 3/4
Hãy tìm sinα, tanα và cotgα
Vì α là góc nhọn nên ta có sinα > 0.
Ta lại có: sin 2 α + cos 2 α = 1
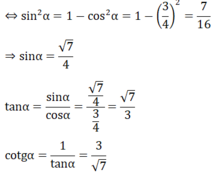
Đúng 0
Bình luận (0)
Tìm cosα, tanα, cotα. biết sinα = 1 5