Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB.
Kẻ AC ⊥ Oy; BD ⊥ Ox. Đường thẳng vuông góc với Ox kẻ từ A cắt đường thẳng vuông góc với
Oy kẻ từ B tại M. Chứng minh OM, AC, BD đồng quy.
HELP ME, THANKS .
MT
Những câu hỏi liên quan
Cho góc nhọn xOy . trên tia Ox lấy điểm A , trên tia Oy lấy điểm B sao cho OA = OB . Từ A hạ AC vuông góc Oy . Từ B hạ BD vuông góc Ox . Chứng minh OC = OD
Cho góc nhọn xoy.TRên tia õ lấy điểm A .trên tia oy lấy diểm B sao cho OA=OB.Kẻ AC vuông góc oy,BD vuông góc Ox.gọi I là giao điểm của AC và BD.
chứng minh tam giác AIB cân.
So sánh IC và IA
a: Xét ΔODB vuông tại D và ΔOCA vuông tại C có
OA=OB
góc O chung
=>ΔODB=ΔOCA
=>OD=OC
=>AD=CB
Xét ΔIDA vuông tại D và ΔICB vuông tại C có
DA=CB
góc IAD=góc IBC
=>ΔIDA=ΔICB
=>IA=IB
b: IA=IB
IB>IC
=>IA>IC
Đúng 0
Bình luận (0)
Cho tam giác xOy nhọn trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Kẻ AH vuông góc với Oy (H thuộc Oy),BK vuông góc Ox(K thuộc Ox)
a. chứng minh tam giác OAH =tam giác OBK
b.chứng minh AH=BK
c.gọi i là giao điểm của AH và BK.chứng minh Oi là tian phân giác của góc xOy
d.gọi M là giao điểm của Oy và AB.chứng minh OM vuông góc AB
e.chứng minh M là trung điểm của AB
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC OD. a) Chứng minh: AD BC. b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho
OA = OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
a) Xét ΔOBC và ΔOAD , có :
góc O chung
OB = OA ( gt )
OC = OD ( gt )
=> ΔOBC = ΔOAD ( c.g.c )
=> AD = BC ( 2 cạnh tương ứng ) ( đpcm )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Đúng 0
Bình luận (1)
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC OD. a) Chứng minh: AD BC. b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho
OA = OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
Đúng 0
Bình luận (0)
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC OD. a) Chứng minh: AD BC. b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho
OA = OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD với BC. Chứng minh: OE là tia phân giác của góc xOy.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
Đúng 0
Bình luận (0)
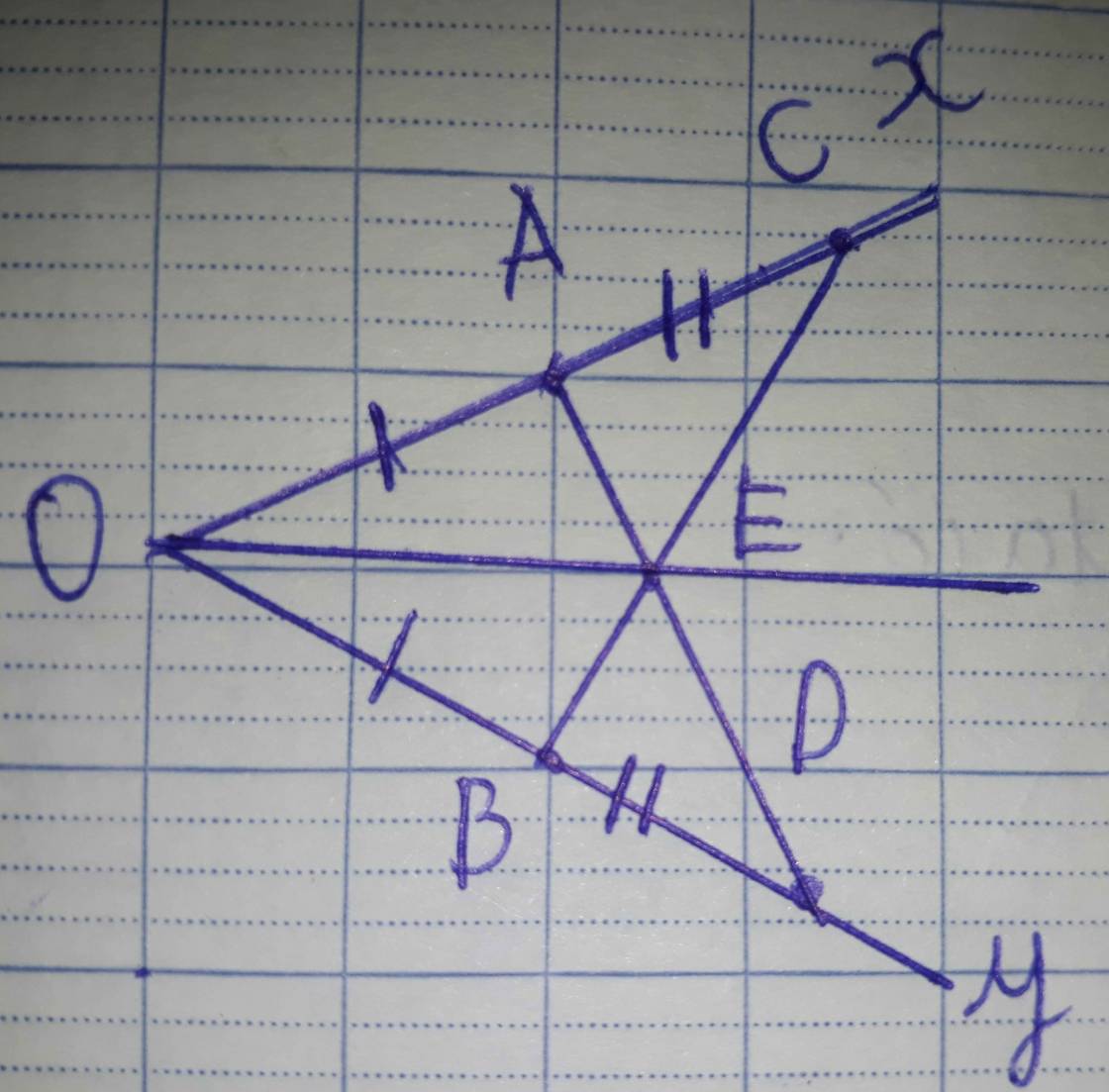
Cho góc nhọn xOy Trên tia ox lấy điểm A trên tia oy lấy diểm B sao cho OA=OB.Trên tia Ax lấy điểm C Trên tia By lấy điểm D sao cho AC=BD a)CM AD=BC. b)gọi E là giao điểm AD và BC.CM △EAC=△EBD. c)CM:OE là phân giác của góc xOy
a) xét ΔOCB và ΔODA, ta có :
OA = OB (giả thiết)
\(\widehat{O}\) là góc chung
AC = BD (giả thiết)
⇒ ΔOCB = ΔODA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
b) xét ΔEAC và ΔEBD, ta có :
AD = BC (câu a)
\(\widehat{AEC}=\widehat{BED}\) (vì là 2 góc đối đỉnh)
AC = BD (giả thiết)
⇒ ΔEAC = ΔEBD (C.G.C)
c) xét ΔOAE và ΔOBE, ta có :
OA = OB (giả thiết)
AE = BE [vì ΔEAC = ΔEBD (2 cạnh tương ứng)]
OE là cạnh chung
⇒ ΔOAE = ΔOBE (c.c.c)
⇒ \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
Đúng 3
Bình luận (0)
Cho tam giác nhọn xOy , trên tia Ox lấy điểm A ( A khác 0 ), trên tia Oy lấy điểm B (B khác 0) sao cho OA=OB. Kẻ AC vuông góc Oy (C thuộc Oy), BD vuông góc Ox (D thuộc Ox) gọi I là giao điểm AC và BD
a) Chứng minh am giác AOC=BOD;
b) Chứng minh tam giác AIB cân
c) so sánh IC và IA
d) chứng minh góc IAB=1/2 AOB
a: Xét ΔAOC vuông tại C và ΔBOD vuông tại D có
OA=OB
góc O chung
=>ΔAOC=ΔBOD
b: góc CAO+góc IAB=góc OAB
góc OBD+góc IBA=góc OBA
mà góc CAO=góc OBD và góc OAB=góc OBA
nên góc IAB=góc IBA
=>ΔIAB cân tại I
c: IC=ID
ID<IA
=>IC<IA
Đúng 0
Bình luận (0)
cho góc nhọn xOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Kẻ đường thẳng vuông góc với Ox tại A cắt Oy tai D.Kẻ đường thẳng vuông góc với Oy tại B cắt Ox Tại C.Giao điểm của AD và BC là E.Nối OE,CD
a)chứng minh OE là phân giác của góc xOy
b)chứng minh tam giác ECD là tam giác cân
c)tia OE cắt CD tại H.Chứng minh OH vuông góc với CD