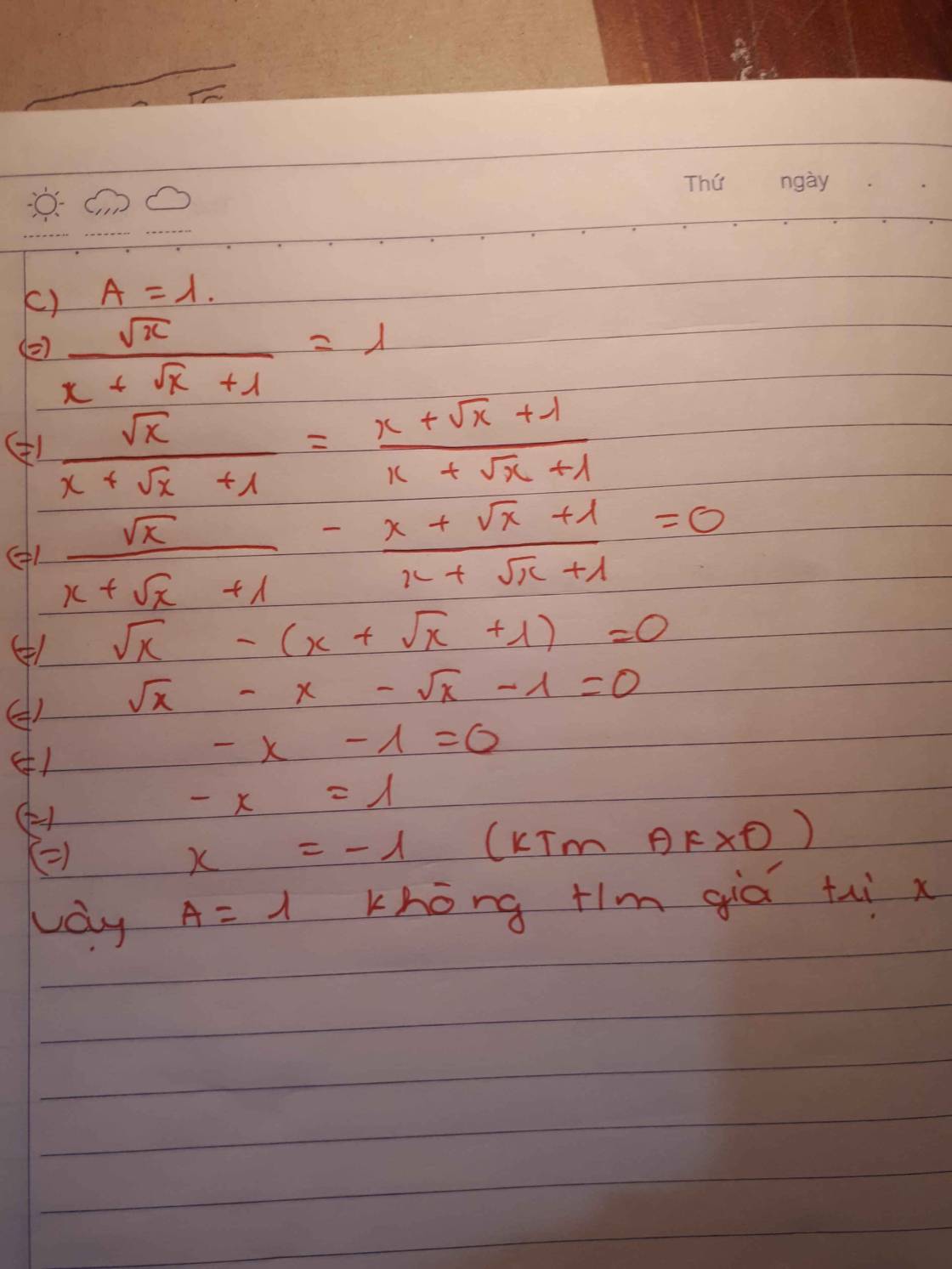mik cần gấp ạ^^

a) \(A=\dfrac{x-4-5-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{x-\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)

b) \(x=6+4\sqrt{2}\Leftrightarrow\sqrt{x}=\sqrt{6+4\sqrt{2}}\)

\(=\sqrt{\left(2+\sqrt{2}\right)^2}=2+\sqrt{2}\)

\(A=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}=\dfrac{2+\sqrt{2}-4}{2+\sqrt{2}-2}=\dfrac{-2+\sqrt{2}}{\sqrt{2}}-\sqrt{2}+1\)

\(a,A=\dfrac{x-4-5-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\left(x\ge0;x\ne4\right)\\ A=\dfrac{x-\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\\ b,x=6+4\sqrt{2}=\left(2+\sqrt{2}\right)^2\Leftrightarrow\sqrt{x}=2+\sqrt{2}\\ \Leftrightarrow A=\dfrac{\sqrt{2}+2-4}{\sqrt{2}+2-2}=\dfrac{\sqrt{2}-2}{\sqrt{2}}=1-\sqrt{2}\)

đk : \(x\ge0,x\ne1\)

\(=>P=\left[\dfrac{2\left(\sqrt{x}+2\right)-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right]:\left[\dfrac{x+\sqrt{x}-2+3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right]\)

\(P=\left[\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right].\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+1}\right]\)

\(P=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)

b,\(x=6-2\sqrt{5}=\left(\sqrt{5}-1\right)^2\) thay vào P

\(=>P=\dfrac{2\sqrt{\left(\sqrt{5}-1\right)^2}-1}{\sqrt{\left(\sqrt{5}-1\right)^2}+1}=\dfrac{2\sqrt{5}-3}{\sqrt{5}}\)

c,\(=>\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}}=>2x-\sqrt{x}=\sqrt{x}+1\)

\(=>2x-2\sqrt{x}-1=0< =>2\left(x-\sqrt{x}-\dfrac{1}{2}\right)=0\)

\(=>x-\sqrt{x}-\dfrac{1}{2}=>\Delta=1-4\left(-\dfrac{1}{2}\right)=3>0=>\left[{}\begin{matrix}x1=\dfrac{1+\sqrt{3}}{2}\\x2=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\)

đối chiếu đk loại x2 còn x1 thỏa

1) ĐKXĐ: \(x\notin\left\{0;1\right\}\)

2) Ta có: \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+1}\right)\)

\(=\dfrac{x+\sqrt{x}+1-\left(x-\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\sqrt{x}+1-3+\sqrt{x}}{\sqrt{x}+1}\)

\(=2\cdot\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

a: Thay \(x=6-2\sqrt{5}\) vào A, ta được:

\(A=1-\dfrac{\sqrt{5}-1}{\sqrt{5}-1+1}=1-\dfrac{\sqrt{5}-1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)

b: Ta có: P=A:B

\(=\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{5\sqrt{x}-10}{x-5\sqrt{x}+6}\right)\)

\(=\dfrac{1}{\sqrt{x}+1}:\dfrac{x-4\sqrt{x}+3-x+4+5\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{1}{\sqrt{x}+1}:\dfrac{1}{\sqrt{x}-2}\)

\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)

\(a,A=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{x-1}\left(dk:x\ge0,x\ne1\right)\)

\(=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)

\(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{x\sqrt{x}-1}\)

\(=\dfrac{x-\sqrt{x}}{x\sqrt{x}-1}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(b,x=14-6\sqrt{5}=\sqrt{5^2}-2.3.\sqrt{5}+3^2=\left(\sqrt{5}-3\right)^2\)

\(\Rightarrow A=\dfrac{\sqrt{\left(\sqrt{5}-3\right)^2}}{14-6\sqrt{5}+\sqrt{\left(\sqrt{5}-3\right)^2}+1}\)

\(=\dfrac{\left|\sqrt{5}-3\right|}{-6\sqrt{5}+15+\left|\sqrt{5}-3\right|}\)

\(=\dfrac{3-\sqrt{5}}{-6\sqrt{5}+15+3-\sqrt{5}}\)

\(=\dfrac{3-\sqrt{5}}{18-7\sqrt{5}}\)

\(c,A=1\Leftrightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}+1}=1\Leftrightarrow\sqrt{x}-x-\sqrt{x}-1=0\Leftrightarrow-x-1=0\Leftrightarrow x=-1\left(ktm\right)\)

Vậy khi A = 1 thì không có giá trị x thỏa mãn.

a) \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+3}\right)\) (ĐK: \(x>0;x\ne1\)) 

\(A=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]:\left(\dfrac{\sqrt{x}+3}{\sqrt{x}+3}-\dfrac{3-\sqrt{x}}{\sqrt{x}+3}\right)\)

\(A=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+3-3+\sqrt{x}}{\sqrt{x}+3}\)

\(A=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}:\dfrac{2\sqrt{x}}{\sqrt{x}+3}\)

\(A=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{2\sqrt{x}}\)

\(A=\dfrac{\sqrt{x}+3}{\sqrt{x}}\)

b) Ta có: \(x=\dfrac{1}{6-2\sqrt{5}}=\dfrac{1}{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot1+1^2}=\dfrac{1}{\left(\sqrt{5}-1\right)^2}=\left(\dfrac{1}{\sqrt{5}-1}\right)^2\)

Thay vào A ta có:

\(A=\dfrac{\sqrt{\left(\dfrac{1}{\sqrt{5}-1}\right)^2}+3}{\sqrt{\left(\dfrac{1}{\sqrt{5}-1}\right)^2}}=3\sqrt{5}-2\)

c) Ta có: \(\dfrac{\sqrt{x}+3}{\sqrt{x}}=1+\dfrac{3}{\sqrt{x}}\)

\(\Rightarrow\sqrt{x}\in\left\{1;3\right\}\)

\(\Rightarrow x\in\left\{1;9\right\}\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x< >1\end{matrix}\right.\)

\(A=\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+3+3-\sqrt{x}}{\sqrt{x}+3}\)

\(=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{6}\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{6}=\dfrac{\sqrt{x}+3}{3}\)

b: Khi \(x=\dfrac{1}{6-2\sqrt{5}}=\dfrac{6+2\sqrt{5}}{16}=\left(\dfrac{\sqrt{5}+1}{4}\right)^2\) thì \(A=\dfrac{\dfrac{\sqrt{5}+1}{4}+3}{3}=\dfrac{\sqrt{5}+1+12}{12}=\dfrac{13+\sqrt{5}}{12}\)

c: A là số nguyên

=>\(\sqrt{x}+3⋮3\)

=>\(\sqrt{x}⋮3\)

=>\(x=k^2\);\(k\in Z\)

Kết hợp ĐKXĐ, ta được: x là số chính phương và x>0 và \(x\ne1\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)

Ta có: \(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\)

\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

Thay \(x=6-2\sqrt{5}\) vào A, ta được:

\(A=\dfrac{\sqrt{5}-1-1}{\sqrt{5}-1+1}=\dfrac{\sqrt{5}-2}{\sqrt{5}}=\dfrac{5-2\sqrt{5}}{5}\)

b: Để \(A< \dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{1}{2}< 0\)

\(\Leftrightarrow2\sqrt{x}-2-\sqrt{x}-1< 0\)

\(\Leftrightarrow x< 9\)

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)