Chứng minh C> 2
Tìm x nguyên để biểu thức C có giá trị nguyên
giúp nhanh nha
Cho A=2(x+1)/x+3
Tìm giá trị nguyên của x để biểu thức A có giá trị nguyên
Giúp mik với nhanh nhé![]()
A∈Z⇒\(\dfrac{2\left(x+1\right)}{x+3}\in Z\Rightarrow\left(2x+2\right)⋮\left(x+3\right)\)
\(\Rightarrow\left(2x+6-4\right)⋮\left(x+3\right)\\ \Rightarrow\left[2\left(x+3\right)-4\right]⋮\left(x+3\right)\)
\(\text{Mà}2\left(x+3\right)⋮\left(x+3\right)\\ \Rightarrow-4⋮\left(x+3\right)\\ \Rightarrow x+3\inƯ\left(-4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\)
- Bạn ơi lớp 6 cũng làm được nhé :)
x ∈{0;-6;-2;-4}
\(A=\dfrac{2\left(x+1\right)}{x+3}=\dfrac{2\left(x+3\right)-4}{x+3}=2-\dfrac{4}{x+3}\)
Để A nguyên \(\Rightarrow\dfrac{4}{x+3}\) nguyên
\(\Rightarrow x+3=Ư\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x=\left\{-7;-5;-4;-2;-1;1\right\}\)
tìm giá trị của x để biểu thức M=\(\dfrac{\sqrt{x}+5}{\sqrt{x}-2}\) có giá trị nguyên
giúp với mk cần gấp
\(M=\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2+7}{\sqrt{x}-2}=1+\dfrac{7}{\sqrt{x}-2}\)
Để M nguyên \(\Leftrightarrow\text{ }7\text{ }⋮\text{ }\left(\sqrt{x}-2\right)\)
=> \(\sqrt{x}-2\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{1;3;9\right\}\)
\(\Rightarrow x\in\left\{1;9;81\right\}\)
bài 1
cho\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)tìm số nguyên x để A có giá trị là một số nguyên
bài 2
tìm giá trị lớn nhất của các biểu thức sau
A=5-(2x-1)\(^2\) B=\(\dfrac{1}{2\cdot\left(x-1\right)^2+3}\) C=\(\dfrac{x^2+8}{x^2+2}\) D=\(\dfrac{1}{\sqrt{x}+3}\)
bài 3 tìm các giá trị nguyên của x để biểu thức sau có giá trị nhỏ nhất
\(A=\dfrac{1}{x-3}\) B\(=\dfrac{7-x}{x-5}\) C\(=\dfrac{5x-19}{x-4}\)
bài 4
ba số a,b,c khác 0 và a+b+c\(\ne\),thỏa mãn điều kiện \(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}\)
tính giá trị biểu thức \(P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\)
Chứng minh A=2x+2/x+3 tìm giá trị nguyên của x để biểu thức trên có giá trị nguyên
\(A=\dfrac{2x+2}{x+3}.\left(x\ne-3\right).\)
\(A=2+\dfrac{-4}{x+3}.\)
Để \(A\in Z.\Leftrightarrow2+\dfrac{-4}{x+3}\in Z.\Leftrightarrow x+3\inƯ\left(-4\right)=\left\{1;-1;2;-2;4;-4\right\}.\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}.\)
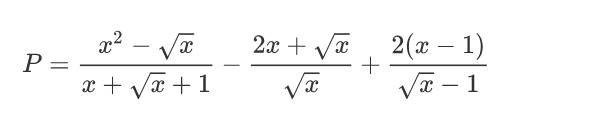
b, tìm x để biểu thức Q=2 căn x/P nhận giá trị là số nguyên
giúp em với ạ
ĐKXĐ: \(x\ne\left\{0;1\right\}\)
Rút gọn được \(P=x-\sqrt{x}+1\)
\(\Rightarrow Q=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
Do \(\left\{{}\begin{matrix}2\sqrt{x}\ge0\\x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow Q\ge0\)
\(Q=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{2\left(x-\sqrt{x}+1\right)-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=2-\dfrac{2\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le2\)
\(\Rightarrow0\le Q\le2\)
Mà \(Q\in Z\Rightarrow Q=\left\{0;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=0\\\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=1\\\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2\sqrt{x}=0\\x-3\sqrt{x}+1=0\\x-2\sqrt{x}+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=\dfrac{3+\sqrt{5}}{2}\\\sqrt{x}=\dfrac{3-\sqrt{5}}{2}\\\sqrt{x}=1\end{matrix}\right.\) \(\Rightarrow x=\left\{0;\dfrac{7+3\sqrt{5}}{2};\dfrac{7-3\sqrt{5}}{2};1\right\}\)
Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.
a) Tính giá trị của biểu thức A khi x = 2/3.
b) Chứng minh B = x−1/x .
c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.
Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.
a) Tính giá trị của biểu thức A khi x = 2/3.
b) Chứng minh B = x−1/x .
c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.
a: Thay x=2/3 vào A, ta được:
\(A=\dfrac{3\cdot\dfrac{2}{3}+2}{\dfrac{2}{3}}=\dfrac{2+2}{\dfrac{2}{3}}=4\cdot\dfrac{3}{2}=6\)
b: \(B=\dfrac{x^2+1}{x^2-x}-\dfrac{2}{x-1}\)
\(=\dfrac{x^2+1}{x\left(x-1\right)}-\dfrac{2}{x-1}\)
\(=\dfrac{x^2+1-2x}{x\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{x\left(x-1\right)}=\dfrac{x-1}{x}\)
c: P=A:B
\(=\dfrac{3x+2}{x}:\dfrac{x-1}{x}=\dfrac{3x+2}{x}\cdot\dfrac{x}{x-1}=\dfrac{3x+2}{x-1}\)
Để P là số nguyên thì \(3x+2⋮x-1\)
=>\(3x-3+5⋮x-1\)
=>\(5⋮x-1\)
=>\(x-1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{2;0;6;-4\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;6;-4\right\}\)
Thay x=2 vào P, ta được:
\(P=\dfrac{3\cdot2+2}{2-1}=\dfrac{8}{1}=8\)
Thay x=6 vào P, ta được:
\(P=\dfrac{3\cdot6+2}{6-1}=\dfrac{18+2}{5}=\dfrac{20}{5}=4\)
Thay x=-4 vào P, ta được:
\(P=\dfrac{3\cdot\left(-4\right)+2}{-4-1}=\dfrac{-12+2}{-5}=\dfrac{-10}{-5}=2\)
Vì 2<4<8
nên khi x=-4 thì P có giá trị nguyên nhỏ nhất
Cho Biểu Thức A= \(\dfrac{3n+2}{n+1}\) (n∈Z,n≠ -1).Tìm giá trị n để A có giá trị nguyên
GIÚP EM VỚI
Để A nguyên thì 3n+3-1 chia hết cho n+1
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)
Cho 2 biểu thức A = \(\dfrac{3x+2}{x}\)và B = \(\dfrac{x^2+1}{x^2-x}-\dfrac{2}{x-1}\)với x≠0, 1.
a) Tính giá trị của biểu thức A khi x = \(\dfrac{2}{3}\) .
b) Chứng minh B = \(\dfrac{x-1}{x}\) .
c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.