Viết PT đường tròn (c) trog trường hợp sau:
đi qua A(1;1) B(1;4) và tiếp xúc trục Ox
Viết PT đường tròn (c) trog trường hợp sau:
đi qua A(1;1) B(1;4) và tiếp xúc trục Ox
Giả sử:I(a;b) là tâm của đường tròn cần tìm.
Ta có: R=d(I;Ox)=|b|
Phương trình đường tròn có dạng
(C):(x–a)2+(y–b)2=b2
Vì (1;1)∈(C) và (1;4)∈(C) nên ta có hệ:\(\left\{{}\begin{matrix}\left(1-a\right)^2+\left(1-b\right)^2=b^2\left(1\right)\\\left(1-a\right)^2+\left(4-b\right)^2=b^2\left(2\right)\end{matrix}\right.\)
Từ hệ trên ta suy ra:(1–b)2=(4–b)2 ⇔ b=\(\dfrac{5}{2}\).
Thay b=\(\dfrac{5}{2}\) vào (1) ta được: a=3,a=−1
Vậy có hai phương trình đường tròn thỏa mãn yêu cầu bài toán
(x–3)2+(y–\(\dfrac{5}{3}\))2=\(\dfrac{25}{4}\)
(x+1)2+(y–\(\dfrac{5}{2}\))2=\(\dfrac{25}{4}\)
1) Viết pt đường tròn tâm l (1,-1) và đi qua điểm B (1,3) 2) Viết pt đường tròn tâm l (3,-4) và đi qua điểm A (1,3) 3) Viết pt đường tròn tâm l ( -2,4) , đi qua điểm B (-6,1) 4) viết pt đường tròn tâm l (1,-2) và đi qua điểm N ( 3,4) Giúp vs bạn
\(A(1;-2),B(3;4),C(-1;0)\)
a) Viết pt đường tròn đi qua A,B và có R=5
b) Viết pt đường tròn đi qua A,B và tiếp xúc với đường thẳng AC
a, Phương trình đường thẳng AB: \(\dfrac{x-3}{2}=\dfrac{y-4}{6}\Leftrightarrow3x-y-5=0\)
Trung điểm I của AB có tọa độ: \(\left\{{}\begin{matrix}x_I=\dfrac{1+3}{2}=2\\y_I=\dfrac{4-2}{2}=1\end{matrix}\right.\Rightarrow I=\left(2;1\right)\)
Phương trình trung trực của AB: \(x+3y-5=0\)
Giả sử \(O=\left(5-3m;m\right)\) là tâm đường tròn
Ta có: \(OA=5\Leftrightarrow\left(3m-4\right)^2+\left(m+2\right)^2=25\)
\(\Leftrightarrow\left(3m-4\right)^2+\left(m+2\right)^2=25\)
\(\Leftrightarrow2m^2-4m-1=0\)
\(\Leftrightarrow m=\dfrac{2\pm\sqrt{6}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}O=\left(\dfrac{4-3\sqrt{6}}{2};\dfrac{2+\sqrt{6}}{2}\right)\\O=\left(\dfrac{4+3\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right)\end{matrix}\right.\)
TH1: \(O=\left(\dfrac{4-3\sqrt{6}}{2};\dfrac{2+\sqrt{6}}{2}\right)\)
Phương trình đường tròn:
\(\left(x-\dfrac{4-3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2+\sqrt{6}}{2}\right)^2=25\)
TH2: \(O=\left(\dfrac{4+3\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right)\)
Phương trình đường tròn:
\(\left(x-\dfrac{4+3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2-\sqrt{6}}{2}\right)^2=25\)
Kết luận: Phương trình đường tròn:
\(\left(x-\dfrac{4-3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2+\sqrt{6}}{2}\right)^2=25\) hoặc \(\left(x-\dfrac{4+3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2-\sqrt{6}}{2}\right)^2=25\)
b, Phương trình đường thẳng AC: \(x+y+1=0\)
Phương trình đường thẳng OA: \(x-y-3=0\)
Giả sử \(O=\left(m;m-3\right)\) là tâm đường tròn
Ta có: \(OA=OB\Leftrightarrow\left(1-m\right)^2+\left(1-m\right)^2=\left(3-m\right)^2+\left(7-m\right)^2\)
\(\Leftrightarrow m=\dfrac{7}{2}\)
\(\Rightarrow O=\left(\dfrac{7}{2};\dfrac{1}{2}\right)\)
Bán kính: \(R=OA=\sqrt{\left(1-\dfrac{7}{2}\right)^2+\left(-2-\dfrac{1}{2}\right)^2}=\dfrac{5\sqrt{2}}{2}\)
Phương trình đường tròn:
\(\left(x-\dfrac{7}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)
cho đường tròn (c) pt: \(\left(x+1\right)^2+y^2=9.\) viết PT đường thẳng đi qua A(2;3) cắt đường tròn (c) tại 2 điểm M,N so cho MN=6
Đường tròn (C) tâm \(I\left(-1;0\right)\) bán kính \(R=3\)
\(MN=6=2R\Rightarrow MN\) là đường kính
\(\Rightarrow\) Đường thẳng d đi qua tâm I của đường tròn
\(\Rightarrow\) Đường thẳng d là đường thẳng IA
\(\overrightarrow{IA}=\left(3;3\right)=3\left(1;1\right)\Rightarrow\) đường thẳng d nhận (1;-1) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow x-y+1=0\)
Cho điểm A(-3;-1), B(2;1), đường thẳng d: x-y+1=0.
a. Tính khoảng cách từ A, B đến đường thẳng d.
b. Viết pt đường thẳng d1 đi qua A và vuông góc với d.
c. Viết phương trình đthẳng d2 đi qua B và song song với d.
d. Viết pt đường tròn (C) có tâm I thuộc d và đi qua 2 điểm A, B
10. Viết pt đường thẳng \(d\) trong các trường hợp sau:
a. \(d\) đi qua 2 điểm \(A,B\) với \(A\left(1;3\right)\) và \(B\left(2;4\right)\)
b.\(d\) đi qua 2 điểm \(C,D\) với \(C\left(-3;2\right)\) và \(D\left(2;3\right)\)
a: (d): y=ax+b
Theo đề, ta có hệ:
a+b=3 và 2a+b=4
=>a=1 và b=2
b: Theo đề, ta có hệ:
-3a+b=2 và 2a+b=3
=>a=1/5 và b=13/5
Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:
A ^ , B ^ , C ^ đều nhọn
A ^ = 90 o
A ^ > 90 o
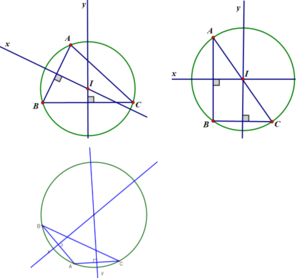
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó.
Để vẽ đường tròn ta cần:
+ Vẽ đường trung trực y của cạnh BC.
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm I bán kính IA.
Nhận xét:
- Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
- Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền (chứng minh bài 56).
- Tam giác tù có tâm đường tròn ngoại tiếp nằm ngoài tam giác.
Giúp mình với ạ Trong mặt phẳng oxy cho tam giác ABC biết A=(2;-3), B=(-1;2),C=(1;-4) a) viết pt tham số của các cạnh tam giác ABC b)Viết pt tổng quát của đuờng cao AH c)Viết pt đường tròn có tâm O đi qua B
Lập pt tham số của đường thẳng d trong trường hợp sau
d đi qua M(1;-4) và có vec tơ chỉ phương u=(2;3)
Phương trình tham số d:
\(\left\{{}\begin{matrix}x=1+2t\\y=-4+3t\end{matrix}\right.\)