 giúp mik nốt câu cảm thụ với
giúp mik nốt câu cảm thụ với
LP
Những câu hỏi liên quan
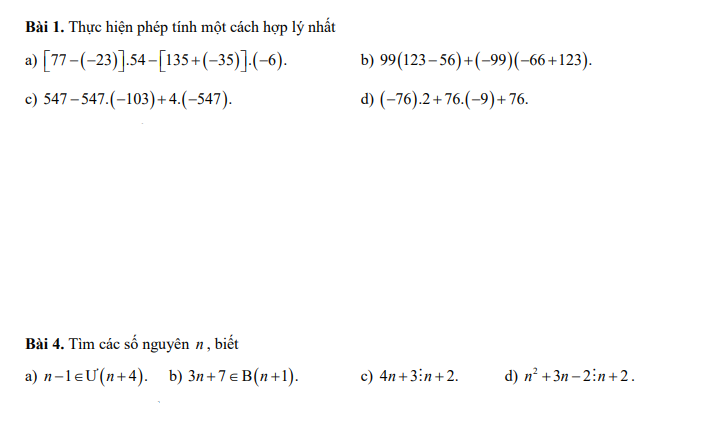
Bạn ILoveMath giúp mik nốt 2 câu này đc ko :))) Mik cảm ơn
Giúp em nốt câu này với ạ em cảm ơn.
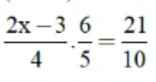
\(\dfrac{2x-3}{4}.\dfrac{6}{5}=\dfrac{21}{10}\\ \Leftrightarrow\dfrac{2x-3}{4}=\dfrac{7}{4}\\ \Leftrightarrow2x-3=7\\ \Leftrightarrow2x=10\\ \Leftrightarrow x=5\)
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
giúp mk làm nốt câu này với,cảm ơn trước nhá
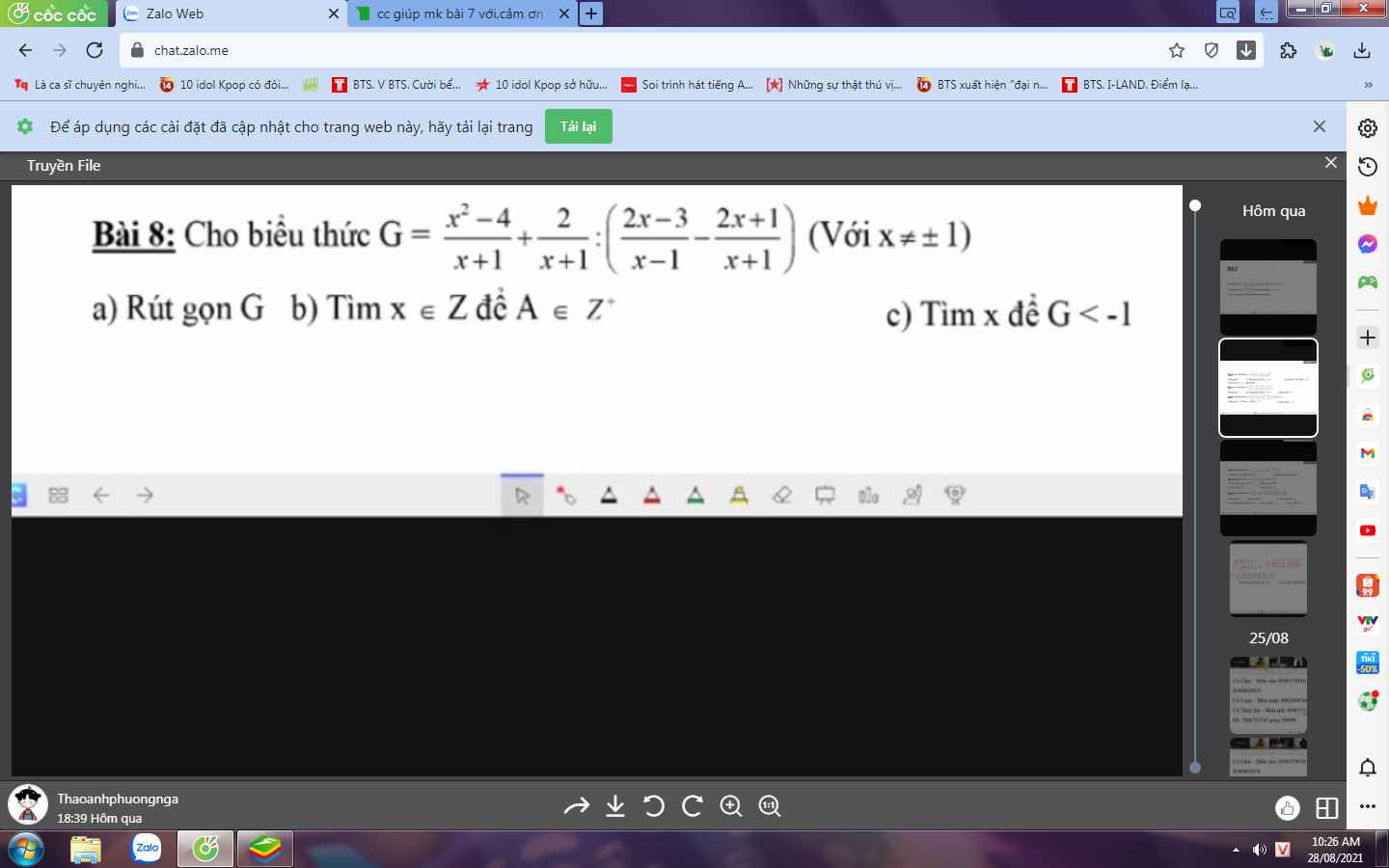
Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
Đúng 1
Bình luận (1)
Bài 8:
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)
Đúng 1
Bình luận (1)
c: Để G<-1 thì G+1<0
\(\Leftrightarrow\dfrac{-3+x+1}{x+1}< 0\)
\(\Leftrightarrow\dfrac{x-2}{x+1}< 0\)
\(\Leftrightarrow-1< x\le2\)
Kết hợp ĐKXĐ, ta được:
\(\left\{{}\begin{matrix}-1< x\le2\\x\ne1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
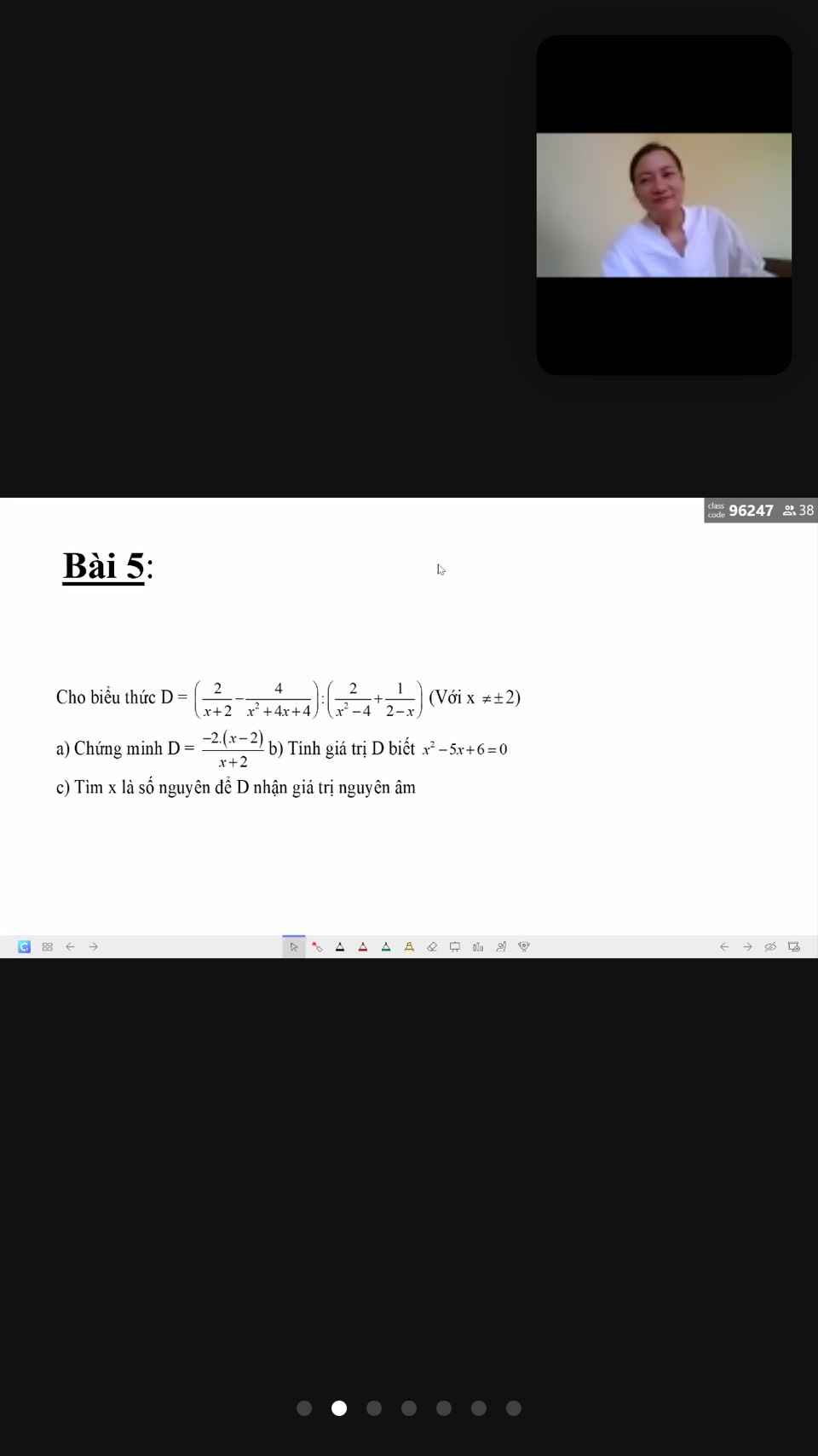 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
Đúng 3
Bình luận (2)
D nguyên âm \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\left(x-2\right)< 0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}-2\left(x-2\right)>0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>2\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\x< -2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x>2\\x< -2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a:Ta có: \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}\cdot\dfrac{\left(x+2\right)\left(x-2\right)}{-x}\)
\(=\dfrac{-\left(x-2\right)}{x+2}\)
b: Ta có: \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
hay x=3
Thay x=3 vào D, ta được:
\(D=\dfrac{-\left(3-2\right)}{3+2}=-\dfrac{1}{5}\)
Đúng 1
Bình luận (1)
 giúp mik nốt câu này rroiif mik pay acc ____
giúp mik nốt câu này rroiif mik pay acc ____
Còn số quãng đường là :
1-2/7-3/8=19/56(quãng đường)
ĐS:...
Đúng 2
Bình luận (0)
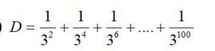
Có anh chị hay thầy cô nào giúp em nốt câu này với ạ, em cảm ơn.
Đề yêu cầu gì vậy em? Rút gọn?
Đúng 2
Bình luận (1)
\(D=\dfrac{1}{3^2}+\dfrac{1}{3^4}+\dfrac{1}{3^6}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow9D=1+\dfrac{1}{3^2}+\dfrac{3}{3^4}+...+\dfrac{1}{3^{98}}\)
\(\Rightarrow9D-D=1-\dfrac{1}{3^{100}}\)
\(\Rightarrow8D=1-\dfrac{1}{3^{100}}\)
\(\Rightarrow D=\dfrac{1}{8}\left(1-\dfrac{1}{3^{100}}\right)\)
Đúng 3
Bình luận (0)

mọi ng giúp mik nốt mấy câu còn lại nha!
1.classmates → classmate
2.are → is
3.good → well
4.to ride → riding
5.in → around
6.Do → Will
7.doing → going
8.interesting → is interesting
9.interest → is interesting
10.played → will play
Đúng 1
Bình luận (0)
3. good → well
4. to ride → riding
5. in → to
6. Do → Will
7. doing → going
8. think → find
9. interest → is interesting
10. played → will play
Đúng 0
Bình luận (0)
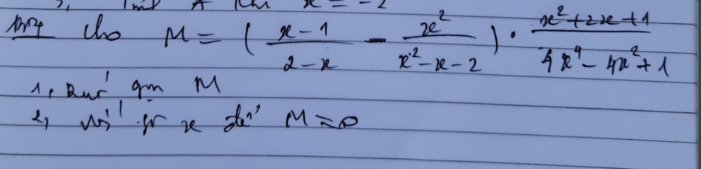
mn ơi giúp mik nốt câu này dc ko ạ plssss
1
Với \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\)
\(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\left(\dfrac{x^2+2x+1}{4x^4-4x^2+1}\right)\\ =\left(\dfrac{\left(x-1\right)\left(x+1\right)}{\left(2-x\right)\left(x+1\right)}+\dfrac{x^2}{\left(x+1\right)\left(2-x\right)}\right)\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{x^2-1+x^2}{\left(x+1\right)\left(2-x\right)}\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{\left(2x^2-1\right)\left(x+1\right)^2}{\left(x+1\right)\left(2-x\right)\left(2x^2-1\right)^2}\\ =\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}\)
2
Để M = 0 thì \(\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}=0\Rightarrow x+1=0\Rightarrow x=-1\) (loại)
Vậy không có giá trị x thỏa mãn M = 0
Đúng 2
Bình luận (0)
1) \(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\cdot\dfrac{x^2+2x+1}{4x^4-4x^2+1}\) (ĐK: \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\))
\(M=\left(\dfrac{-\left(x-1\right)}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x^2-1\right)-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-2x^2+1}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(2x^2-1\right)\left(x+1\right)^2}{\left(x-2\right)\left(x+1\right)\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}\)
2) Ta có: \(M=0\)
\(\Rightarrow\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}=0\)
\(\Leftrightarrow-\left(x+1\right)=0\)
\(\Leftrightarrow-x=1\)
\(\Leftrightarrow x=-1\left(ktm\right)\)
Đúng 1
Bình luận (0)
1: \(M=\left(\dfrac{-x+1}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(=\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(=\dfrac{1-2x^2}{\left(x-2\right)}\cdot\dfrac{x+1}{\left(1-2x^2\right)^2}=\dfrac{x+1}{\left(x-2\right)\left(1-2x^2\right)}\)
2: M=0
=>x+1=0
=>x=-1(loại)
Đúng 0
Bình luận (0)
Lấp La Lấp Lánh trả lời giúp mik nốt câu này đc ko bn?







