cho tam giác ABC (A=90);từ trung điểm E của cạnh AC kẻ EFv vuông góc với BC. nối AF và BE
a, cmr:AF=BE.cos C
b, biết BC =10cm, sin C=0.6 . tính diện tích tứ giác ABFE
c, AF và BE cắt nhau tại O. tính sin góc AOB
H24
Những câu hỏi liên quan
Cho tam giác ABC có A < 90 ,ngoài tam giác ABC ve tam giác MAB và NAC vuông cân tại A . CMR MC vuông góc NB
Cho tam giác ABC ( góc A < 90 độ) . Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân (cân tại A) Và AEC (cân tại A)
a, CMR : BE=CD
b, Cmr : BE vuông góc với CD
Cho góc xOy = 90 độ. Lấy E thuộc Oy, D thuộc Oxsao cho góc DAE =90 độ trong đó A là 1 điểm thuộc phân giác Oz của góc xOy. CMR tam giác DAE cân
Cho tam giác ABC ( AB < AC), góc A =40 độ. Kẻ phân giác AD của góc BAC, lất M thuộc AC sao cho góc MDC = 40 độ. CMR tam giác BDM cân
cho tam giác ABC có A^=90 độ , B^=50 độ . tia phân giác trong của tam giác ABC tại đỉnh B cắt tia phân giác ngoài tại đỉnh C ở điểm O . Tính số đo góc BOC và góc AOB
Cho tam giác ABC có góc A < 90o. Vẽ ra ngoài tam giác ABC các tam giác vuông cân tại A là tam giác ABM và tam giác ACN.
a, Chứng minh tam giác AMC = ANB
b, Chứng minh BN vuông góc với CM
c, Kẻ AH vuông góc BC (H thuộc BC). Chứng minh AH đi qua trung điểm của MN
có góc MAB = góc NAC = 90
góc MAB + gpcs BAC = góc MAC
góc NAC + góc BAC = góc BAN
=> góc MAC = góc BAN
xét tam giác MAC và tam giác BAN có :
MA = MB do tam giác MAB cân tại A (gt)
AN = AC do tam giác ANC cân tại A (gt)
=> tam giác MAC = tam giác BAN (c-g-c)
b, gọi MC cắt BA tại I và MC cắt BN tại E
xét tam giác MIA vuông tại A => góc AMI + góc MIA = 90
có góc AMI = góc IBE do tam giác MAC = tam giác BAN (Câu a)
góc MIA = góc BIE (đối đỉnh)
=> góc BIE + góc IBE = 90
=> tam giác BIE vuông tại E
=> MC _|_ BN
c,
Cho tam giác ABC : B^ = 90 độ
Kẻ phân giác AD ( D thuộc BC)
Kẻ DE vuông góc AC (E thuộc AC)
a) C/m tam giác BAD = tam giác BED
b) Kéo dài DE cắt AB tại K. C/m AK = AC.
a: Xét ΔBAD vuông tại B và ΔBED vuông tại E có
AD chung
\(\widehat{BAD}=\widehat{EAD}\)
Do đó: ΔBAD=ΔBED
b: Xét ΔBDK vuông tại B và ΔEDC vuông tại E có
DB=DE
\(\widehat{BDK}=\widehat{EDC}\)
Do đó: ΔBDK=ΔEDC
Suy ra: BK=EC
Ta có: AB+BK=AK
AE+EC=AC
mà AB=AE
và BK=EC
nên AK=AC
Đúng 1
Bình luận (0)
Cho tam giác ABC , góc A < 90 , ngoài tam giác ABC vẽ tam giác NAC vuông cân tại A .
CMR : MC vuông góc NB .
Làm ơn giúp nhanh nha các bn !!!!!!
mk đang gấp
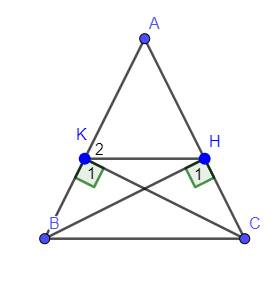
cho tam giác ABC cân tại A ( A < 90˚ ) kẻ BC vuông góc với AC tại H , CK vuông góc với AB tại K
a) chứng minh hai tam giác BHC = CKB từ đó tam giác AHK cân
b) chứng minh BC // HK
`a)`
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
Đúng 1
Bình luận (0)
Giúp mik nhanh voi cho tam giác ABC là tam giác đều, góc giữa 2 vectơ (vectơ AC , vectơ CB) bằng
A 60° B 120° C 30° D 90°
Xem chi tiết
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng :HBHC
b) Chứng minh rằng: AH là tia phân giác của góc A
Bài 2: Cho tam giác ABC cân tại A có góc A 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại N
a) Chứng minh AM AN
b) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc A.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng :HB=HC
b) Chứng minh rằng: AH là tia phân giác của góc A
Bài 2: Cho tam giác ABC cân tại A có góc A < 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại N
a) Chứng minh AM= AN
b) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc A.